Question Number 72694 by MJS last updated on 31/Oct/19
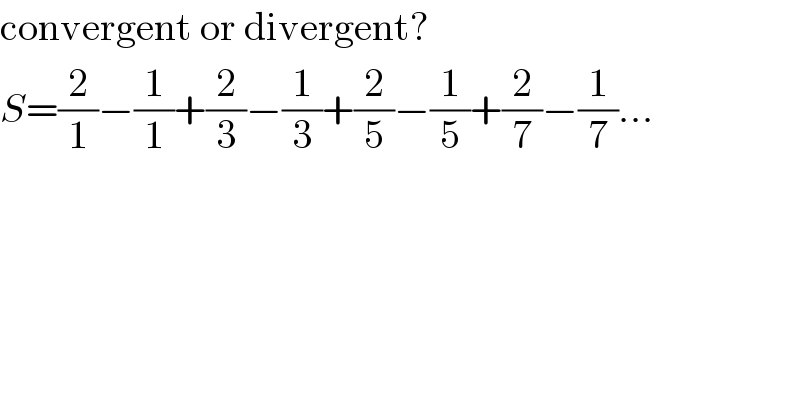
$$\mathrm{convergent}\:\mathrm{or}\:\mathrm{divergent}? \\ $$$${S}=\frac{\mathrm{2}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{7}}… \\ $$
Commented by mathmax by abdo last updated on 31/Oct/19
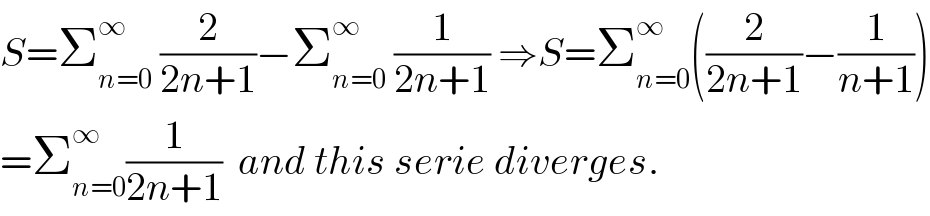
$${S}=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:\Rightarrow{S}=\sum_{{n}=\mathrm{0}} ^{\infty} \left(\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:\:{and}\:{this}\:{serie}\:{diverges}. \\ $$
Commented by MJS last updated on 31/Oct/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mathmax by abdo last updated on 31/Oct/19
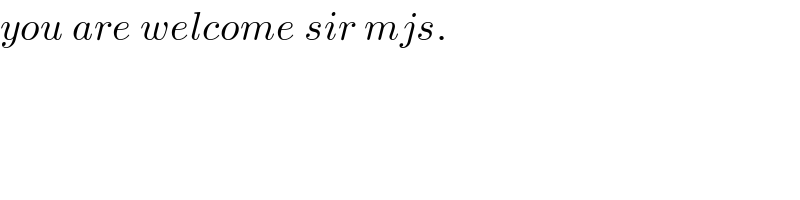
$${you}\:{are}\:{welcome}\:{sir}\:{mjs}. \\ $$
