Menu Close

cos-1-x-3-x-1-cos-1-x-x-3-cos-1-1-y-2pi-3-find-the-value-of-y-

Tinku Tara
Pin




Question Number 131301 by liberty last updated on 03/Feb/21
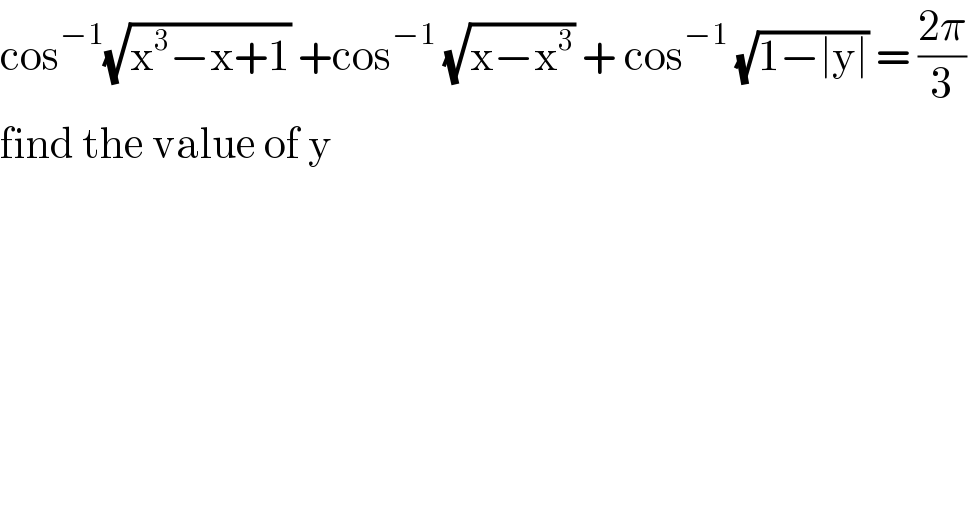
cos^(−1) (√(x^3 −x+1)) +cos^(−1) (√(x−x^3 )) + cos^(−1) (√(1−∣y∣)) = ((2π)/3) find the value of y
$$\mathrm{cos}^{−\mathrm{1}} \sqrt{\mathrm{x}^{\mathrm{3}} −\mathrm{x}+\mathrm{1}}\:+\mathrm{cos}^{−\mathrm{1}} \:\sqrt{\mathrm{x}−\mathrm{x}^{\mathrm{3}} }\:+\:\mathrm{cos}^{−\mathrm{1}} \:\sqrt{\mathrm{1}−\mid\mathrm{y}\mid}\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{y}\: \\ $$
Answered by EDWIN88 last updated on 03/Feb/21
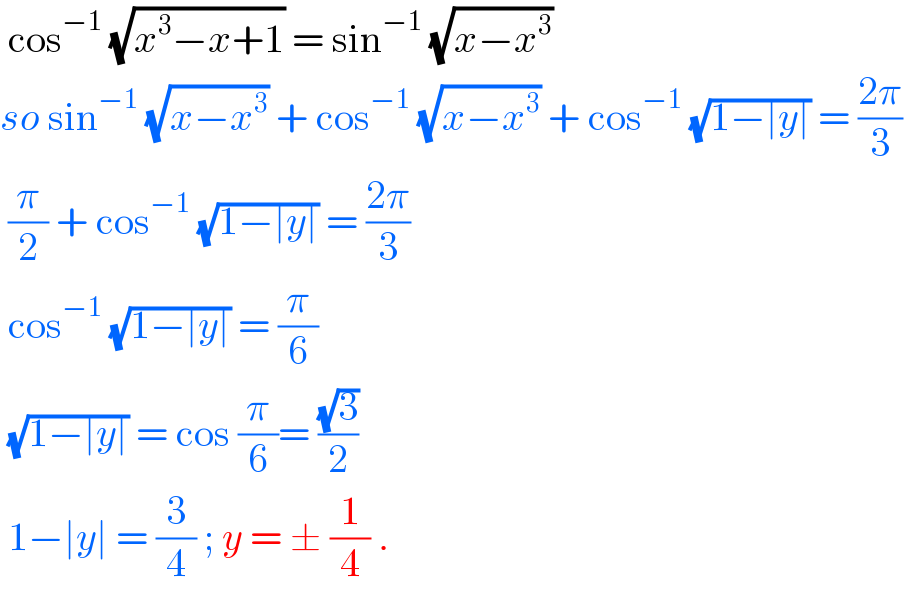
cos^(−1) (√(x^3 −x+1)) = sin^(−1) (√(x−x^3 )) so sin^(−1) (√(x−x^3 )) + cos^(−1) (√(x−x^3 )) + cos^(−1) (√(1−∣y∣)) = ((2π)/3) (π/2) + cos^(−1) (√(1−∣y∣)) = ((2π)/3) cos^(−1) (√(1−∣y∣)) = (π/6) (√(1−∣y∣)) = cos (π/6)= ((√3)/2) 1−∣y∣ = (3/4) ; y = ± (1/4) .
$$\:\mathrm{cos}^{−\mathrm{1}} \:\sqrt{{x}^{\mathrm{3}} −{x}+\mathrm{1}}\:=\:\mathrm{sin}^{−\mathrm{1}} \:\sqrt{{x}−{x}^{\mathrm{3}} } \\ $$$${so}\:\mathrm{sin}^{−\mathrm{1}} \:\sqrt{{x}−{x}^{\mathrm{3}} }\:+\:\mathrm{cos}^{−\mathrm{1}} \:\sqrt{{x}−{x}^{\mathrm{3}} }\:+\:\mathrm{cos}^{−\mathrm{1}} \:\sqrt{\mathrm{1}−\mid{y}\mid}\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\:\frac{\pi}{\mathrm{2}}\:+\:\mathrm{cos}^{−\mathrm{1}} \:\sqrt{\mathrm{1}−\mid{y}\mid}\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\:\mathrm{cos}^{−\mathrm{1}} \:\sqrt{\mathrm{1}−\mid{y}\mid}\:=\:\frac{\pi}{\mathrm{6}} \\ $$$$\:\sqrt{\mathrm{1}−\mid{y}\mid}\:=\:\mathrm{cos}\:\frac{\pi}{\mathrm{6}}=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\mathrm{1}−\mid{y}\mid\:=\:\frac{\mathrm{3}}{\mathrm{4}}\:;\:{y}\:=\:\pm\:\frac{\mathrm{1}}{\mathrm{4}}\:. \\ $$

Pin