Menu Close

cos-2-ln-cos-sin-cos-sin-

Tinku Tara 0 Comments
Pin




Question Number 76963 by peter frank last updated on 01/Jan/20
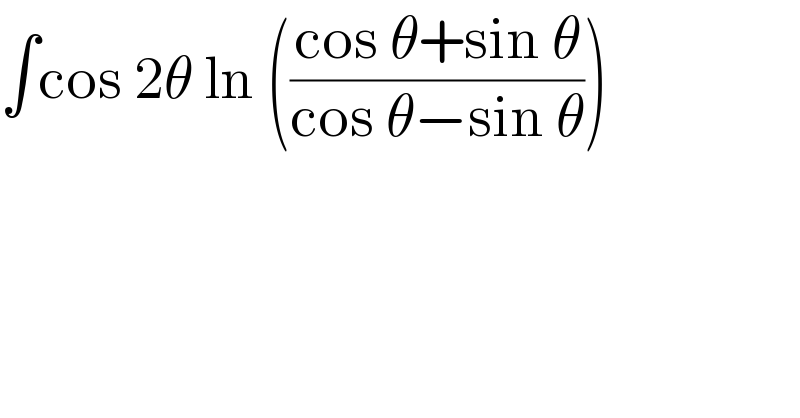
∫cos 2θ ln (((cos θ+sin θ)/(cos θ−sin θ)))
$$\int\mathrm{cos}\:\mathrm{2}\theta\:\mathrm{ln}\:\left(\frac{\mathrm{cos}\:\theta+\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta−\mathrm{sin}\:\theta}\right) \\ $$
Answered by MJS last updated on 02/Jan/20
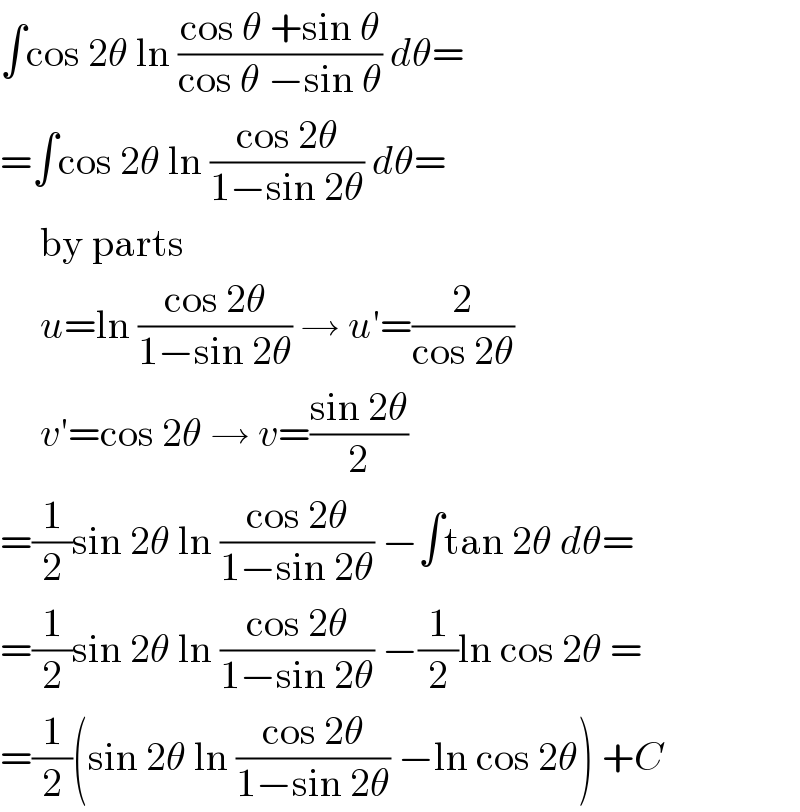
∫cos 2θ ln ((cos θ +sin θ)/(cos θ −sin θ)) dθ= =∫cos 2θ ln ((cos 2θ)/(1−sin 2θ)) dθ= by parts u=ln ((cos 2θ)/(1−sin 2θ)) → u′=(2/(cos 2θ)) v′=cos 2θ → v=((sin 2θ)/2) =(1/2)sin 2θ ln ((cos 2θ)/(1−sin 2θ)) −∫tan 2θ dθ= =(1/2)sin 2θ ln ((cos 2θ)/(1−sin 2θ)) −(1/2)ln cos 2θ = =(1/2)(sin 2θ ln ((cos 2θ)/(1−sin 2θ)) −ln cos 2θ) +C
$$\int\mathrm{cos}\:\mathrm{2}\theta\:\mathrm{ln}\:\frac{\mathrm{cos}\:\theta\:+\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta\:−\mathrm{sin}\:\theta}\:{d}\theta= \\ $$$$=\int\mathrm{cos}\:\mathrm{2}\theta\:\mathrm{ln}\:\frac{\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}−\mathrm{sin}\:\mathrm{2}\theta}\:{d}\theta= \\ $$$$\:\:\:\:\:\mathrm{by}\:\mathrm{parts} \\ $$$$\:\:\:\:\:{u}=\mathrm{ln}\:\frac{\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}−\mathrm{sin}\:\mathrm{2}\theta}\:\rightarrow\:{u}'=\frac{\mathrm{2}}{\mathrm{cos}\:\mathrm{2}\theta} \\ $$$$\:\:\:\:\:{v}'=\mathrm{cos}\:\mathrm{2}\theta\:\rightarrow\:{v}=\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{ln}\:\frac{\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}−\mathrm{sin}\:\mathrm{2}\theta}\:−\int\mathrm{tan}\:\mathrm{2}\theta\:{d}\theta= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{ln}\:\frac{\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}−\mathrm{sin}\:\mathrm{2}\theta}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{cos}\:\mathrm{2}\theta\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{ln}\:\frac{\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}−\mathrm{sin}\:\mathrm{2}\theta}\:−\mathrm{ln}\:\mathrm{cos}\:\mathrm{2}\theta\right)\:+{C} \\ $$
Commented by john santu last updated on 02/Jan/20
Commented by john santu last updated on 02/Jan/20
to Mr MJS
$${to}\:{Mr}\:{MJS}\: \\ $$
Commented by peter frank last updated on 02/Jan/20
thank you
$${thank}\:{you} \\ $$
Commented by MJS last updated on 02/Jan/20
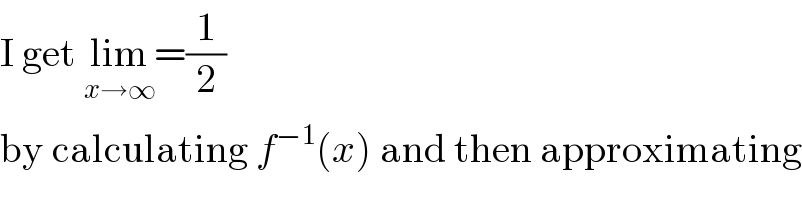
I get lim_(x→∞) =(1/2) by calculating f^(−1) (x) and then approximating
$$\mathrm{I}\:\mathrm{get}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{by}\:\mathrm{calculating}\:{f}^{−\mathrm{1}} \left({x}\right)\:\mathrm{and}\:\mathrm{then}\:\mathrm{approximating} \\ $$
Commented by jagoll last updated on 02/Jan/20
how sir? please your write
$$\mathrm{how}\:\mathrm{sir}?\:\mathrm{please}\:\mathrm{your}\:\mathrm{write} \\ $$$$ \\ $$
Commented by MJS last updated on 02/Jan/20
y=8x^3 +3x exchanging x⇌y y^3 +(3/8)y−(x/8)=0 D=(p^3 /(27))+(q^2 /4)=(1/(512))+(x^2 /(256))≥0∀y∈R ⇒ Cardano′s firmula ⇒ f^(−1) (x)=(1/(2(4)^(1/3) ))(((2x+(√(4x^2 +2))))^(1/3) −((−2x+(√(4x^2 +2))))^(1/3) ) g(x)=((f^(−1) (8x)−f^(−1) (x))/x^(1/3) ) g(10^1 )=.526706... g(10^2 )=.505799... g(10^3 )=.501249... g(10^4 )=.500269... g(10^5 )=.500058... ...
$${y}=\mathrm{8}{x}^{\mathrm{3}} +\mathrm{3}{x} \\ $$$$\mathrm{exchanging}\:{x}\rightleftharpoons{y} \\ $$$${y}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{8}}{y}−\frac{{x}}{\mathrm{8}}=\mathrm{0} \\ $$$${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{512}}+\frac{{x}^{\mathrm{2}} }{\mathrm{256}}\geqslant\mathrm{0}\forall{y}\in\mathbb{R}\:\Rightarrow\:\mathrm{Cardano}'\mathrm{s}\:\mathrm{firmula} \\ $$$$\Rightarrow \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{4}}}\left(\sqrt[{\mathrm{3}}]{\mathrm{2}{x}+\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}}}−\sqrt[{\mathrm{3}}]{−\mathrm{2}{x}+\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}}}\right) \\ $$$${g}\left({x}\right)=\frac{{f}^{−\mathrm{1}} \left(\mathrm{8}{x}\right)−{f}^{−\mathrm{1}} \left({x}\right)}{{x}^{\mathrm{1}/\mathrm{3}} } \\ $$$${g}\left(\mathrm{10}^{\mathrm{1}} \right)=.\mathrm{526706}… \\ $$$${g}\left(\mathrm{10}^{\mathrm{2}} \right)=.\mathrm{505799}… \\ $$$${g}\left(\mathrm{10}^{\mathrm{3}} \right)=.\mathrm{501249}… \\ $$$${g}\left(\mathrm{10}^{\mathrm{4}} \right)=.\mathrm{500269}… \\ $$$${g}\left(\mathrm{10}^{\mathrm{5}} \right)=.\mathrm{500058}… \\ $$$$… \\ $$
Commented by MJS last updated on 02/Jan/20
...I do not understand your method...
$$…\mathrm{I}\:\mathrm{do}\:\mathrm{not}\:\mathrm{understand}\:\mathrm{your}\:\mathrm{method}… \\ $$
Commented by jagoll last updated on 02/Jan/20
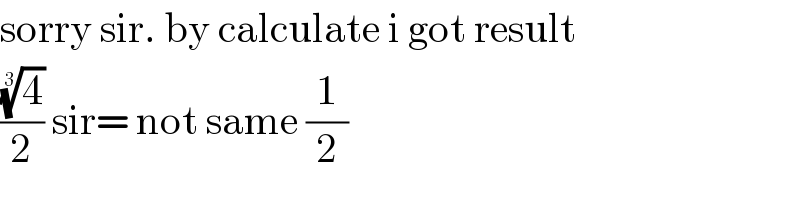
sorry sir. by calculate i got result ((4)^(1/3) /2) sir= not same (1/2)
$$\mathrm{sorry}\:\mathrm{sir}.\:\mathrm{by}\:\mathrm{calculate}\:\mathrm{i}\:\mathrm{got}\:\mathrm{result} \\ $$$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{4}}}{\mathrm{2}}\:\mathrm{sir}=\:\mathrm{not}\:\mathrm{same}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 02/Jan/20
to john santu sir: your step to lim_(x→∞) [(8/(24(g(x))^2 +3))−(1/(24(h(x))^2 ×3))]×3x^(2/3) is correct. but this doesn′t help you further, since g(x)=f^( −1) (8x) and h(x)=f^( −1) (x) are still unknown. your last step to =3×[(8/(24))−(1/(24))] is wrong. how can you get this if you don′t explictly know g(x) and h(x)?
$${to}\:{john}\:{santu}\:{sir}: \\ $$$${your}\:{step}\:{to} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\mathrm{8}}{\mathrm{24}\left({g}\left({x}\right)\right)^{\mathrm{2}} +\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{24}\left({h}\left({x}\right)\right)^{\mathrm{2}} ×\mathrm{3}}\right]×\mathrm{3}{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$${is}\:{correct}.\:{but}\:{this}\:{doesn}'{t}\:{help}\:{you} \\ $$$${further},\:{since}\:{g}\left({x}\right)={f}^{\:−\mathrm{1}} \left(\mathrm{8}{x}\right)\:{and} \\ $$$${h}\left({x}\right)={f}^{\:−\mathrm{1}} \left({x}\right)\:{are}\:{still}\:{unknown}. \\ $$$${your}\:{last}\:{step}\:{to} \\ $$$$=\mathrm{3}×\left[\frac{\mathrm{8}}{\mathrm{24}}−\frac{\mathrm{1}}{\mathrm{24}}\right] \\ $$$${is}\:{wrong}.\:{how}\:{can}\:{you}\:{get}\:{this}\:{if} \\ $$$${you}\:{don}'{t}\:{explictly}\:{know}\:{g}\left({x}\right)\:{and} \\ $$$${h}\left({x}\right)? \\ $$
Commented by john santu last updated on 02/Jan/20
ok sir, i agree. i thought the degrees g(x) and h(x) were the same, but forgot the coefficients that might not be equal to 1.
$${ok}\:{sir},\:{i}\:{agree}.\:{i}\:{thought}\:{the}\:{degrees}\: \\ $$$${g}\left({x}\right)\:{and}\:{h}\left({x}\right)\:{were}\:{the}\:{same},\:{but}\: \\ $$$${forgot}\:{the}\:{coefficients}\:{that}\:{might}\: \\ $$$${not}\:{be}\:{equal}\:{to}\:\mathrm{1}.\: \\ $$
Commented by mr W last updated on 02/Jan/20
the degrees of g(x) and h(x) could be the same, but you have here (g(x))^2 and (h(x))^2 , and we don′t even know the degrees of them. therefore we don′t know the values of lim_(x→∞) (((g(x))^2 )/x^(2/3) ) and lim_(x→∞) (((h(x))^2 )/x^(2/3) ).
$${the}\:{degrees}\:{of}\:{g}\left({x}\right)\:{and}\:{h}\left({x}\right)\:{could} \\ $$$${be}\:{the}\:{same},\:{but}\:{you}\:{have}\:{here} \\ $$$$\left({g}\left({x}\right)\right)^{\mathrm{2}} \:{and}\:\left({h}\left({x}\right)\right)^{\mathrm{2}} ,\:{and}\:{we}\:{don}'{t} \\ $$$${even}\:{know}\:{the}\:{degrees}\:{of}\:{them}. \\ $$$${therefore}\:{we}\:{don}'{t}\:{know}\:{the}\:{values}\:{of} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left({g}\left({x}\right)\right)^{\mathrm{2}} }{{x}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:{and}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left({h}\left({x}\right)\right)^{\mathrm{2}} }{{x}^{\frac{\mathrm{2}}{\mathrm{3}}} }. \\ $$
Commented by jagoll last updated on 03/Jan/20
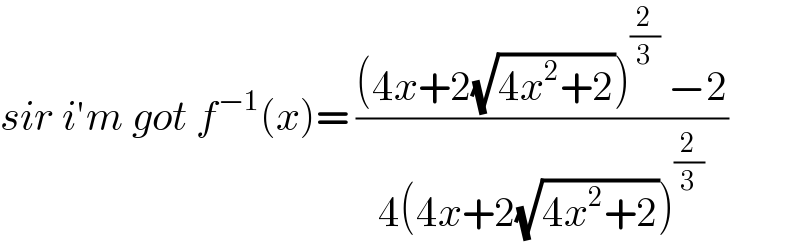
sir i′m got f^(−1) (x)= (((4x+2(√(4x^2 +2)))^(2/3) −2)/(4(4x+2(√(4x^2 +2)))^(2/3) ))
$${sir}\:{i}'{m}\:{got}\:{f}^{−\mathrm{1}} \left({x}\right)=\:\frac{\left(\mathrm{4}{x}+\mathrm{2}\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:−\mathrm{2}}{\mathrm{4}\left(\mathrm{4}{x}+\mathrm{2}\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} } \\ $$
Commented by MJS last updated on 03/Jan/20
how? x^3 +px+q=0 Cardano′s solution x=u+v u=((−(q/2)+(√((p^3 /(27))+(q^2 /4)))))^(1/3) v=((−(q/2)−(√((p^3 /(27))+(q^2 /4)))))^(1/3) u, v ∈R (some calculators give the “wrong” root i.e. ((−8))^(1/3) =−2 but ((8e^(iπ) ))^(1/3) =(8)^(1/3) e^(i(π/3)) =1+i(√3))
$$\mathrm{how}? \\ $$$${x}^{\mathrm{3}} +{px}+{q}=\mathrm{0} \\ $$$$\mathrm{Cardano}'\mathrm{s}\:\mathrm{solution} \\ $$$${x}={u}+{v} \\ $$$${u}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}} \\ $$$${v}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}−\sqrt{\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}} \\ $$$${u},\:{v}\:\in\mathbb{R} \\ $$$$\left(\mathrm{some}\:\mathrm{calculators}\:\mathrm{give}\:\mathrm{the}\:“\mathrm{wrong}''\:\mathrm{root}\right. \\ $$$$\left.\mathrm{i}.\mathrm{e}.\:\sqrt[{\mathrm{3}}]{−\mathrm{8}}=−\mathrm{2}\:\mathrm{but}\:\sqrt[{\mathrm{3}}]{\mathrm{8e}^{\mathrm{i}\pi} }=\sqrt[{\mathrm{3}}]{\mathrm{8}}\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{3}}} =\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *