cos-3-x-sinx-dx-

Question Number 5262 by Kasih last updated on 03/May/16

\int \cos^{3} x \sqrt{\sin x} d x

Answered by Yozzii last updated on 03/May/16

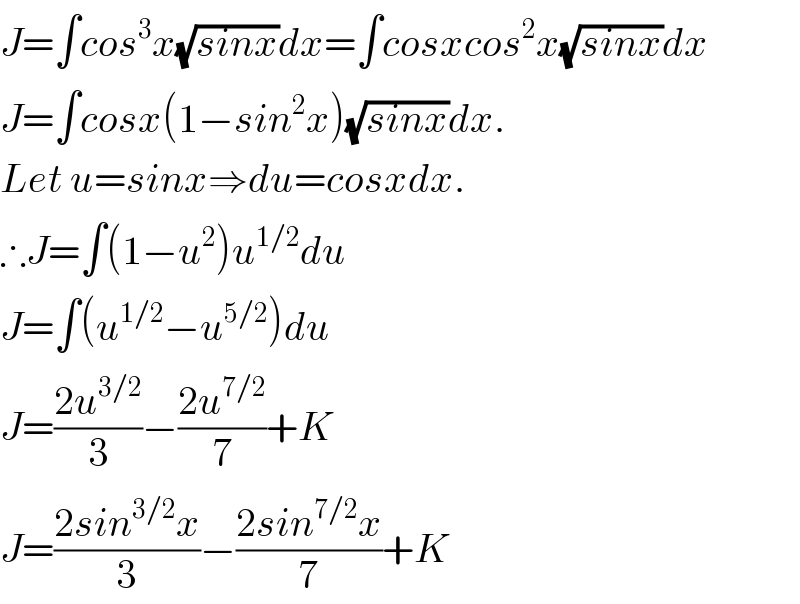
J = \int {c o s}^{3} x \sqrt{s i n x} d x = \int {c o s x c o s}^{2} x \sqrt{s i n x} d x

J = \int c o s x (1 - {s i n}^{2} x) \sqrt{s i n x} d x .

L e t u = s i n x \Rightarrow d u = c o s x d x .

∴ J = \int (1 - u^{2}) u^{1 / 2} d u

J = \int (u^{1 / 2} - u^{5 / 2}) d u

J = \frac{2 u^{3 / 2}}{3} - \frac{2 u^{7 / 2}}{7} + K

J = \frac{2 {s i n}^{3 / 2} x}{3} - \frac{2 {s i n}^{7 / 2} x}{7} + K

Facebook Tweet Pin