Question Number 11147 by suci last updated on 14/Mar/17

$$\int{cos}^{\mathrm{4}} {x}\:{sinx}\:{dx}=….??? \\ $$
Answered by ajfour last updated on 14/Mar/17

$$=\:−\frac{\mathrm{cos}\:^{\mathrm{5}} {x}}{\mathrm{5}}+{C}\: \\ $$
Commented by ajfour last updated on 14/Mar/17
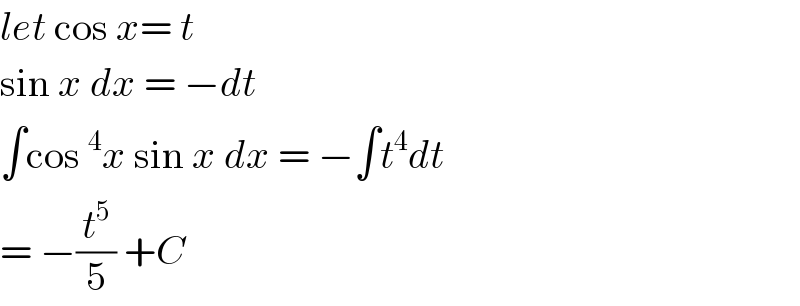
$${let}\:\mathrm{cos}\:{x}=\:{t} \\ $$$$\mathrm{sin}\:{x}\:{dx}\:=\:−{dt} \\ $$$$\int\mathrm{cos}\:^{\mathrm{4}} {x}\:\mathrm{sin}\:{x}\:{dx}\:=\:−\int{t}^{\mathrm{4}} {dt} \\ $$$$=\:−\frac{{t}^{\mathrm{5}} }{\mathrm{5}}\:+{C} \\ $$
Answered by Mechas88 last updated on 17/Mar/17

$$\int{cos}\mathrm{4}{xsinxdx}= \\ $$$$\int\frac{\mathrm{1}}{\mathrm{2}}\left({sin}\left({x}+\mathrm{4}{x}\right)+{sin}\left({x}−\mathrm{4}{x}\right)\right){dx}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int{sin}\mathrm{5}{xdx}+\mathrm{1}/\mathrm{2}\int{sin}−\mathrm{3}{xdx}= \\ $$$$ \\ $$$$−\frac{{cos}\mathrm{5}{x}}{\mathrm{10}}\:+\frac{\mathrm{1}}{\mathrm{2}}×\:\frac{{cos}\mathrm{3}{x}}{\mathrm{3}}\:+{C} \\ $$$$ \\ $$$$\frac{{cos}\mathrm{3}{x}}{\mathrm{6}}\:−\frac{{cos}\mathrm{5}{x}}{\mathrm{10}}\:+{C} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
