Menu Close

cos-6-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 7898 by tawakalitu last updated on 23/Sep/16
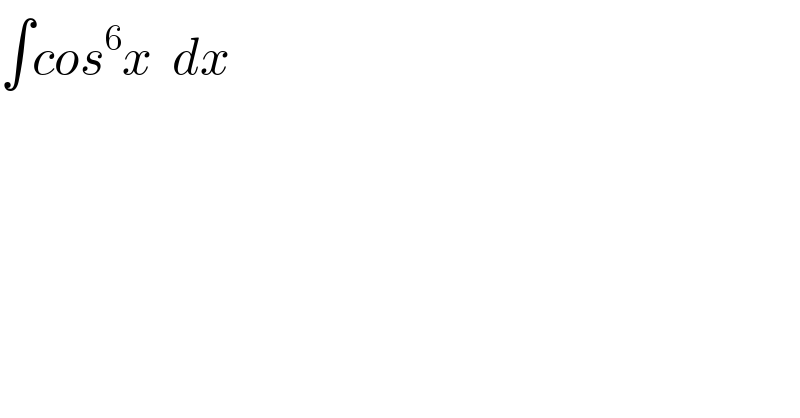
∫cos^6 x dx
$$\int{cos}^{\mathrm{6}} {x}\:\:{dx} \\ $$
Commented by sandy_suhendra last updated on 24/Sep/16
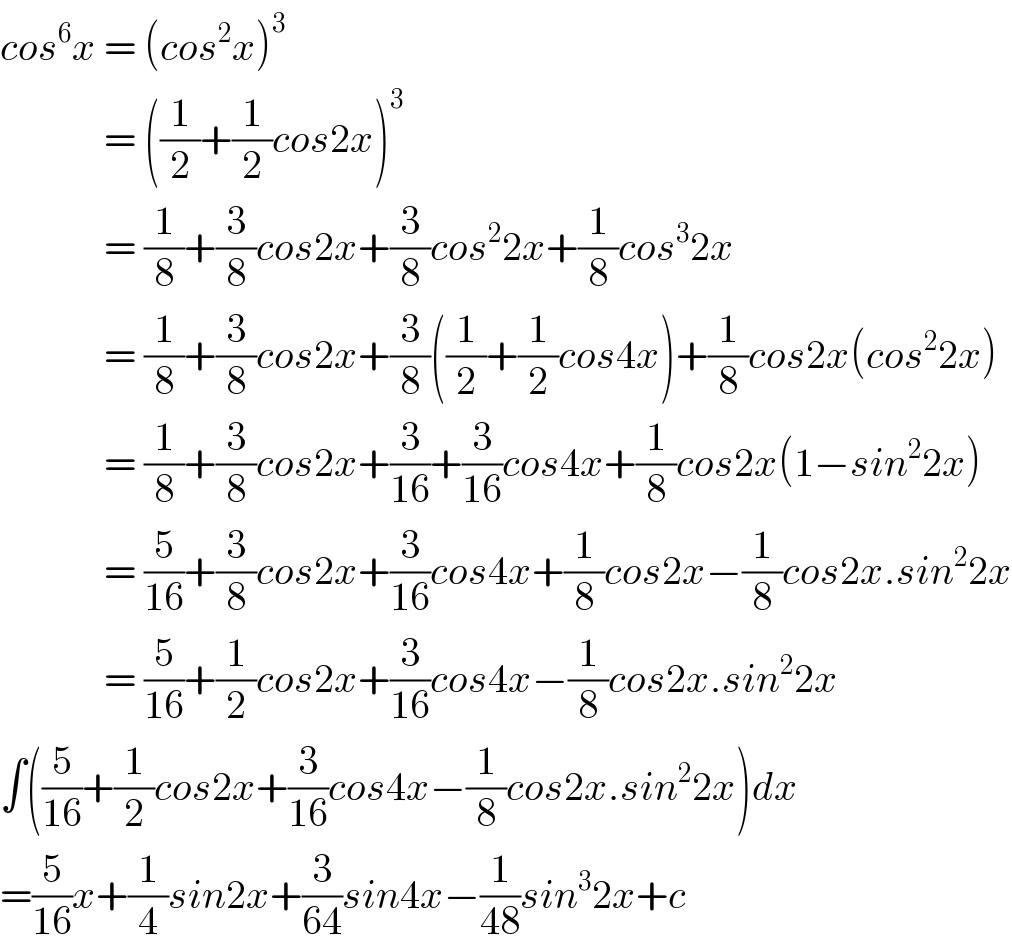
cos^6 x = (cos^2 x)^3 = ((1/2)+(1/2)cos2x)^3 = (1/8)+(3/8)cos2x+(3/8)cos^2 2x+(1/8)cos^3 2x = (1/8)+(3/8)cos2x+(3/8)((1/2)+(1/2)cos4x)+(1/8)cos2x(cos^2 2x) = (1/8)+(3/8)cos2x+(3/(16))+(3/(16))cos4x+(1/8)cos2x(1−sin^2 2x) = (5/(16))+(3/8)cos2x+(3/(16))cos4x+(1/8)cos2x−(1/8)cos2x.sin^2 2x = (5/(16))+(1/2)cos2x+(3/(16))cos4x−(1/8)cos2x.sin^2 2x ∫((5/(16))+(1/2)cos2x+(3/(16))cos4x−(1/8)cos2x.sin^2 2x)dx =(5/(16))x+(1/4)sin2x+(3/(64))sin4x−(1/(48))sin^3 2x+c
$${cos}^{\mathrm{6}} {x}\:=\:\left({cos}^{\mathrm{2}} {x}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{cos}\mathrm{2}{x}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{3}}{\mathrm{8}}{cos}\mathrm{2}{x}+\frac{\mathrm{3}}{\mathrm{8}}{cos}^{\mathrm{2}} \mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{8}}{cos}^{\mathrm{3}} \mathrm{2}{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{3}}{\mathrm{8}}{cos}\mathrm{2}{x}+\frac{\mathrm{3}}{\mathrm{8}}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{cos}\mathrm{4}{x}\right)+\frac{\mathrm{1}}{\mathrm{8}}{cos}\mathrm{2}{x}\left({cos}^{\mathrm{2}} \mathrm{2}{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{3}}{\mathrm{8}}{cos}\mathrm{2}{x}+\frac{\mathrm{3}}{\mathrm{16}}+\frac{\mathrm{3}}{\mathrm{16}}{cos}\mathrm{4}{x}+\frac{\mathrm{1}}{\mathrm{8}}{cos}\mathrm{2}{x}\left(\mathrm{1}−{sin}^{\mathrm{2}} \mathrm{2}{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{5}}{\mathrm{16}}+\frac{\mathrm{3}}{\mathrm{8}}{cos}\mathrm{2}{x}+\frac{\mathrm{3}}{\mathrm{16}}{cos}\mathrm{4}{x}+\frac{\mathrm{1}}{\mathrm{8}}{cos}\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{8}}{cos}\mathrm{2}{x}.{sin}^{\mathrm{2}} \mathrm{2}{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{5}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{2}}{cos}\mathrm{2}{x}+\frac{\mathrm{3}}{\mathrm{16}}{cos}\mathrm{4}{x}−\frac{\mathrm{1}}{\mathrm{8}}{cos}\mathrm{2}{x}.{sin}^{\mathrm{2}} \mathrm{2}{x} \\ $$$$\int\left(\frac{\mathrm{5}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{2}}{cos}\mathrm{2}{x}+\frac{\mathrm{3}}{\mathrm{16}}{cos}\mathrm{4}{x}−\frac{\mathrm{1}}{\mathrm{8}}{cos}\mathrm{2}{x}.{sin}^{\mathrm{2}} \mathrm{2}{x}\right){dx} \\ $$$$=\frac{\mathrm{5}}{\mathrm{16}}{x}+\frac{\mathrm{1}}{\mathrm{4}}{sin}\mathrm{2}{x}+\frac{\mathrm{3}}{\mathrm{64}}{sin}\mathrm{4}{x}−\frac{\mathrm{1}}{\mathrm{48}}{sin}^{\mathrm{3}} \mathrm{2}{x}+{c} \\ $$
Commented by tawakalitu last updated on 24/Sep/16
Thanks for your help.
$${Thanks}\:{for}\:{your}\:{help}. \\ $$
Answered by prakash jain last updated on 02/Oct/16
$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *