Question Number 4783 by Dnilka228 last updated on 10/Mar/16
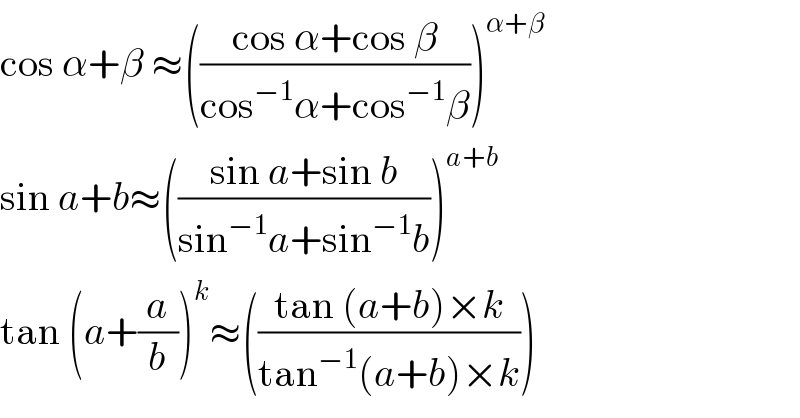
$$\mathrm{cos}\:\alpha+\beta\:\approx\left(\frac{\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta}{\mathrm{cos}^{−\mathrm{1}} \alpha+\mathrm{cos}^{−\mathrm{1}} \beta}\right)^{\alpha+\beta} \\ $$$$\mathrm{sin}\:{a}+{b}\approx\left(\frac{\mathrm{sin}\:{a}+\mathrm{sin}\:{b}}{\mathrm{sin}^{−\mathrm{1}} {a}+\mathrm{sin}^{−\mathrm{1}} {b}}\right)^{{a}+{b}} \\ $$$$\mathrm{tan}\:\left({a}+\frac{{a}}{{b}}\right)^{{k}} \approx\left(\frac{\mathrm{tan}\:\left({a}+{b}\right)×{k}}{\mathrm{tan}^{−\mathrm{1}} \left({a}+{b}\right)×{k}}\right) \\ $$
Commented by Dnilka228 last updated on 10/Mar/16
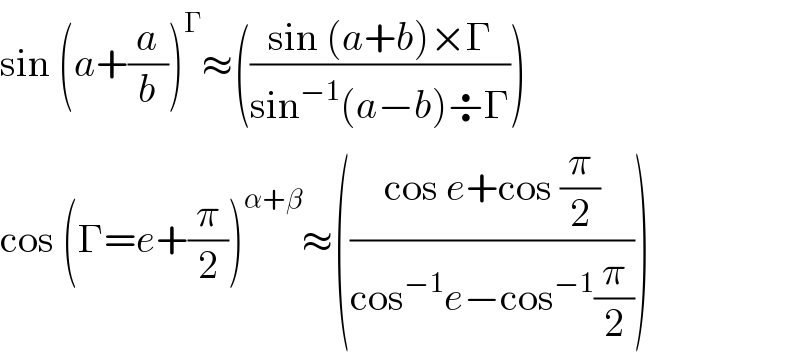
$$\mathrm{sin}\:\left({a}+\frac{{a}}{{b}}\right)^{\Gamma} \approx\left(\frac{\mathrm{sin}\:\left({a}+{b}\right)×\Gamma}{\mathrm{sin}^{−\mathrm{1}} \left({a}−{b}\right)\boldsymbol{\div}\Gamma}\right) \\ $$$$\mathrm{cos}\:\left(\Gamma={e}+\frac{\pi}{\mathrm{2}}\right)^{\alpha+\beta} \approx\left(\frac{\mathrm{cos}\:{e}+\mathrm{cos}\:\frac{\pi}{\mathrm{2}}}{\mathrm{cos}^{−\mathrm{1}} {e}−\mathrm{cos}^{−\mathrm{1}} \frac{\pi}{\mathrm{2}}}\right) \\ $$
