Question Number 143810 by Jamshidbek last updated on 18/Jun/21
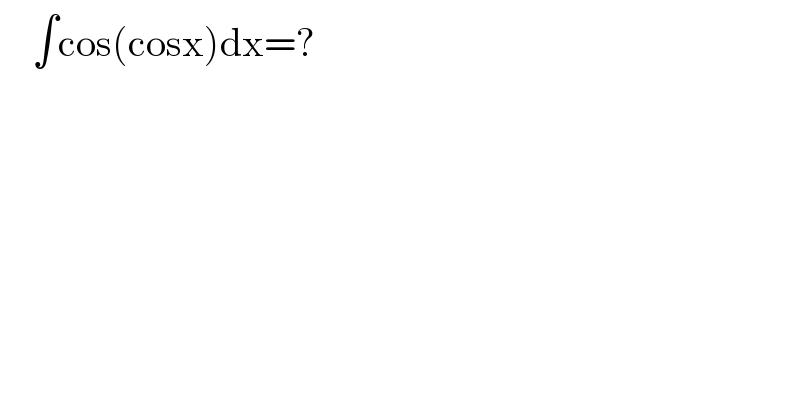
$$\:\:\:\:\int\mathrm{cos}\left(\mathrm{cosx}\right)\mathrm{dx}=? \\ $$
Answered by mathmax by abdo last updated on 18/Jun/21
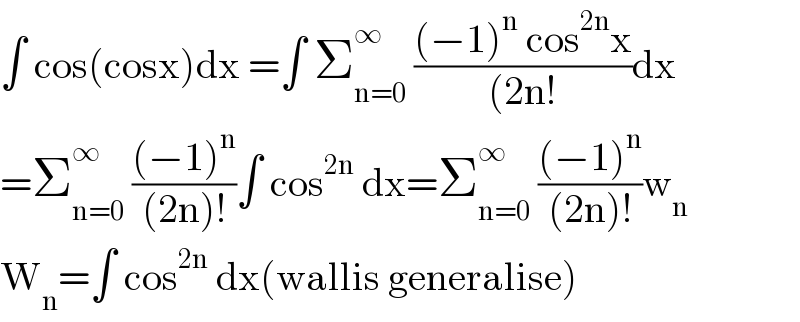
$$\int\:\mathrm{cos}\left(\mathrm{cosx}\right)\mathrm{dx}\:=\int\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{cos}^{\mathrm{2n}} \mathrm{x}}{\left(\mathrm{2n}!\right.}\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}\right)!}\int\:\mathrm{cos}^{\mathrm{2n}} \:\mathrm{dx}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}\right)!}\mathrm{w}_{\mathrm{n}} \\ $$$$\mathrm{W}_{\mathrm{n}} =\int\:\mathrm{cos}^{\mathrm{2n}} \:\mathrm{dx}\left(\mathrm{wallis}\:\mathrm{generalise}\right) \\ $$
Answered by mathmax by abdo last updated on 19/Jun/21
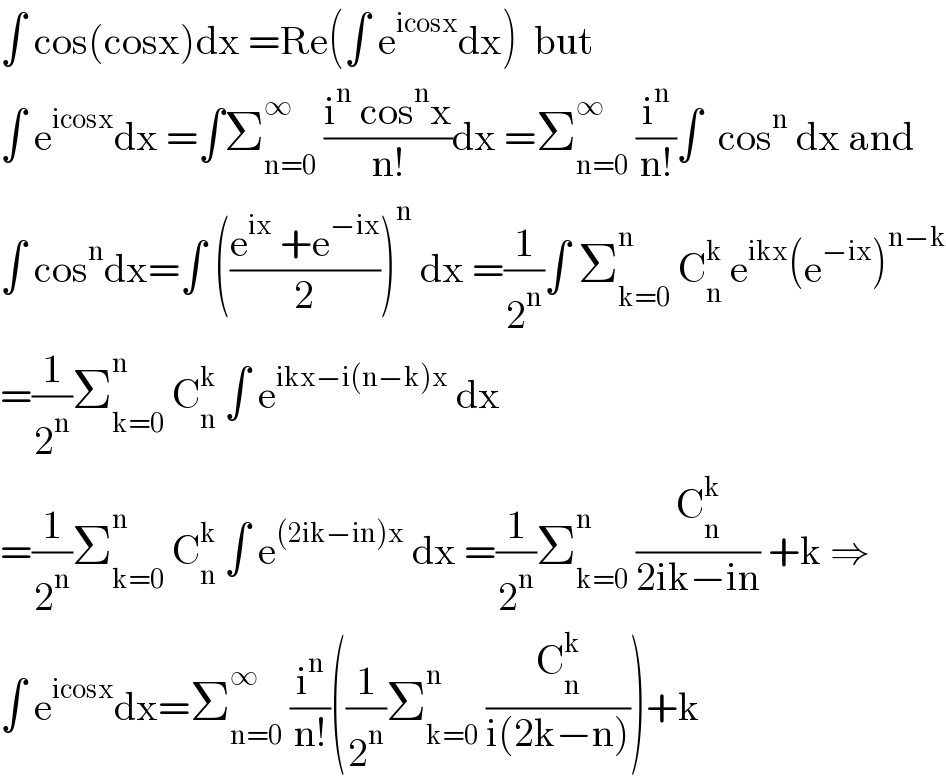
$$\int\:\mathrm{cos}\left(\mathrm{cosx}\right)\mathrm{dx}\:=\mathrm{Re}\left(\int\:\mathrm{e}^{\mathrm{icosx}} \mathrm{dx}\right)\:\:\mathrm{but} \\ $$$$\int\:\mathrm{e}^{\mathrm{icosx}} \mathrm{dx}\:=\int\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{i}^{\mathrm{n}} \:\mathrm{cos}^{\mathrm{n}} \mathrm{x}}{\mathrm{n}!}\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{i}^{\mathrm{n}} }{\mathrm{n}!}\int\:\:\mathrm{cos}^{\mathrm{n}} \:\mathrm{dx}\:\mathrm{and} \\ $$$$\int\:\mathrm{cos}^{\mathrm{n}} \mathrm{dx}=\int\:\left(\frac{\mathrm{e}^{\mathrm{ix}} \:+\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2}}\right)^{\mathrm{n}} \:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\int\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{ikx}} \left(\mathrm{e}^{−\mathrm{ix}} \right)^{\mathrm{n}−\mathrm{k}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\int\:\mathrm{e}^{\mathrm{ikx}−\mathrm{i}\left(\mathrm{n}−\mathrm{k}\right)\mathrm{x}} \:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\int\:\mathrm{e}^{\left(\mathrm{2ik}−\mathrm{in}\right)\mathrm{x}} \:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\mathrm{2ik}−\mathrm{in}}\:+\mathrm{k}\:\Rightarrow \\ $$$$\int\:\mathrm{e}^{\mathrm{icosx}} \mathrm{dx}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{i}^{\mathrm{n}} }{\mathrm{n}!}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)}\right)+\mathrm{k} \\ $$
Commented by mathmax by abdo last updated on 20/Jun/21
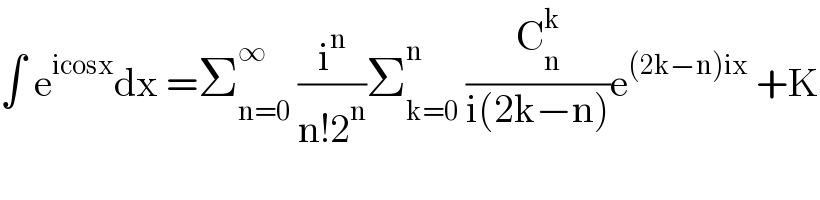
$$\int\:\mathrm{e}^{\mathrm{icosx}} \mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{i}^{\mathrm{n}} }{\mathrm{n}!\mathrm{2}^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)}\mathrm{e}^{\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{ix}} \:+\mathrm{K} \\ $$
