Question Number 131176 by Raxreedoroid last updated on 02/Feb/21
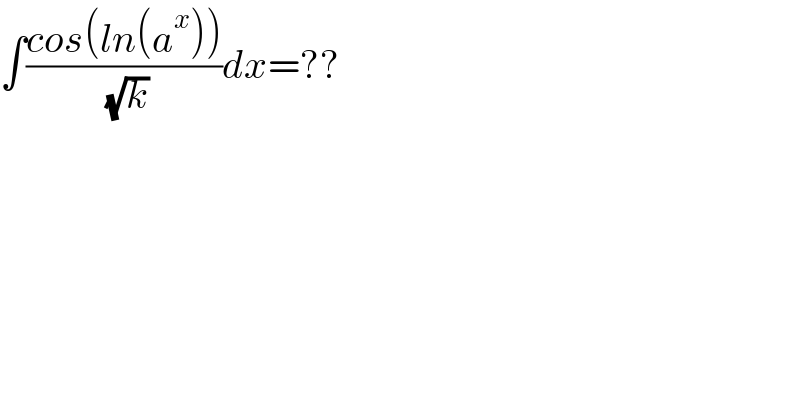
$$\int\frac{{cos}\left({ln}\left({a}^{{x}} \right)\right)}{\:\sqrt{{k}}}{dx}=?? \\ $$
Answered by Ar Brandon last updated on 02/Feb/21
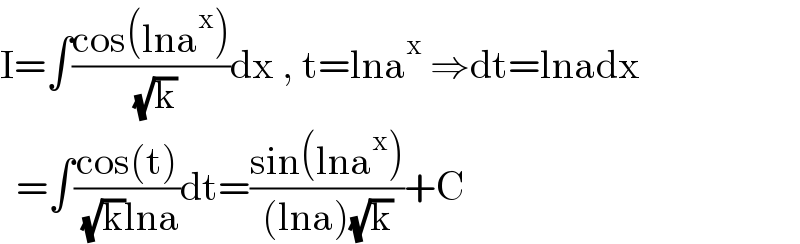
$$\mathrm{I}=\int\frac{\mathrm{cos}\left(\mathrm{lna}^{\mathrm{x}} \right)}{\:\sqrt{\mathrm{k}}}\mathrm{dx}\:,\:\mathrm{t}=\mathrm{lna}^{\mathrm{x}} \:\Rightarrow\mathrm{dt}=\mathrm{lnadx} \\ $$$$\:\:=\int\frac{\mathrm{cos}\left(\mathrm{t}\right)}{\:\sqrt{\mathrm{k}}\mathrm{lna}}\mathrm{dt}=\frac{\mathrm{sin}\left(\mathrm{lna}^{\mathrm{x}} \right)}{\left(\mathrm{lna}\right)\sqrt{\mathrm{k}}}+\mathrm{C} \\ $$
