Question Number 9515 by Joel575 last updated on 12/Dec/16
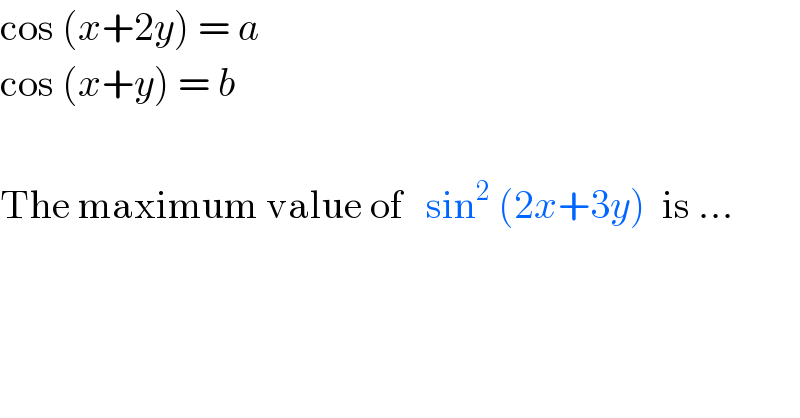
$$\mathrm{cos}\:\left({x}+\mathrm{2}{y}\right)\:=\:{a} \\ $$$$\mathrm{cos}\:\left({x}+{y}\right)\:=\:{b} \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{of}\:\:\:\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{2}{x}+\mathrm{3}{y}\right)\:\:\mathrm{is}\:… \\ $$
Answered by mrW last updated on 15/Dec/16
![sin^2 (2x+3y)=[sin (x+2y+x+y)]^2 =[sin (x+2y)cos (x+y)+cos (x+2y)sin (x+y)]^2 =[b×sin (x+2y)+a×sin (x+y)]^2 =b^2 ×sin^2 (x+2y)+2ab×sin (x+2y)×sin (x+y)+a^2 ×sin^2 (x+y) =b^2 (1−a^2 )+2ab×sin (x+2y)×sin (x+y)+a^2 (1−b^2 ) =a^2 +b^2 −2a^2 b^2 +2ab×sin (x+2y)×sin (x+y) =a^2 +b^2 −2a^2 b^2 ±2ab(√((1−a^2 )(1−b^2 ))) max=a^2 +b^2 −2a^2 b^2 +2∣ab∣(√((1−a^2 )(1−b^2 ))) min=a^2 +b^2 −2a^2 b^2 −2∣ab∣(√((1−a^2 )(1−b^2 )))](https://www.tinkutara.com/question/Q9518.png)
$$\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{2}{x}+\mathrm{3}{y}\right)=\left[\mathrm{sin}\:\left(\mathrm{x}+\mathrm{2y}+\mathrm{x}+\mathrm{y}\right)\right]^{\mathrm{2}} \\ $$$$=\left[\mathrm{sin}\:\left(\mathrm{x}+\mathrm{2y}\right)\mathrm{cos}\:\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{cos}\:\left(\mathrm{x}+\mathrm{2y}\right)\mathrm{sin}\:\left(\mathrm{x}+\mathrm{y}\right)\right]^{\mathrm{2}} \\ $$$$=\left[\mathrm{b}×\mathrm{sin}\:\left(\mathrm{x}+\mathrm{2y}\right)+\mathrm{a}×\mathrm{sin}\:\left(\mathrm{x}+\mathrm{y}\right)\right]^{\mathrm{2}} \\ $$$$=\mathrm{b}^{\mathrm{2}} ×\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{x}+\mathrm{2y}\right)+\mathrm{2ab}×\mathrm{sin}\:\left(\mathrm{x}+\mathrm{2y}\right)×\mathrm{sin}\:\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{a}^{\mathrm{2}} ×\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{x}+\mathrm{y}\right) \\ $$$$=\mathrm{b}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)+\mathrm{2ab}×\mathrm{sin}\:\left(\mathrm{x}+\mathrm{2y}\right)×\mathrm{sin}\:\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{a}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{b}^{\mathrm{2}} \right) \\ $$$$=\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{2ab}×\mathrm{sin}\:\left(\mathrm{x}+\mathrm{2y}\right)×\mathrm{sin}\:\left(\mathrm{x}+\mathrm{y}\right) \\ $$$$=\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \pm\mathrm{2ab}\sqrt{\left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{b}^{\mathrm{2}} \right)} \\ $$$$\mathrm{max}=\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{2}\mid\mathrm{ab}\mid\sqrt{\left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{b}^{\mathrm{2}} \right)} \\ $$$$\mathrm{min}=\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} −\mathrm{2}\mid\mathrm{ab}\mid\sqrt{\left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{b}^{\mathrm{2}} \right)} \\ $$
Commented by Joel575 last updated on 12/Dec/16
$${thank}\:{you}\:{very}\:{much} \\ $$
