Question Number 11245 by uni last updated on 18/Mar/17

$${cos}\mathrm{10}×{cos}\mathrm{20}×{cos}\mathrm{40}=? \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 18/Mar/17
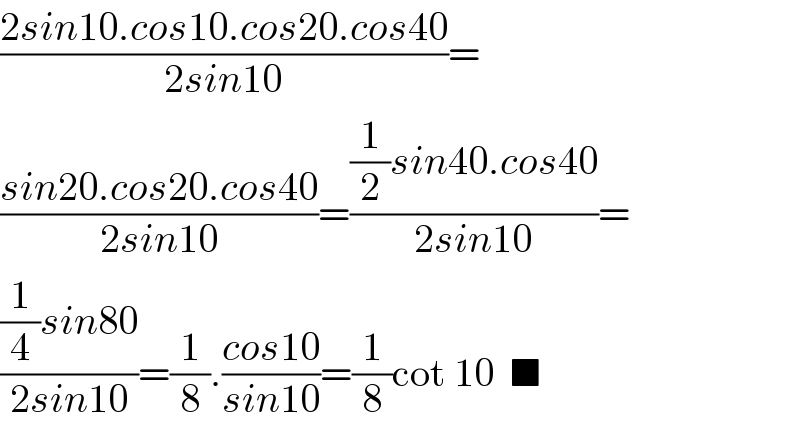
$$\frac{\mathrm{2}{sin}\mathrm{10}.{cos}\mathrm{10}.{cos}\mathrm{20}.{cos}\mathrm{40}}{\mathrm{2}{sin}\mathrm{10}}= \\ $$$$\frac{{sin}\mathrm{20}.{cos}\mathrm{20}.{cos}\mathrm{40}}{\mathrm{2}{sin}\mathrm{10}}=\frac{\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{40}.{cos}\mathrm{40}}{\mathrm{2}{sin}\mathrm{10}}= \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{4}}{sin}\mathrm{80}}{\mathrm{2}{sin}\mathrm{10}}=\frac{\mathrm{1}}{\mathrm{8}}.\frac{{cos}\mathrm{10}}{{sin}\mathrm{10}}=\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cot}\:\mathrm{10}\:\:\blacksquare \\ $$
