Question Number 138315 by LUFFY last updated on 12/Apr/21
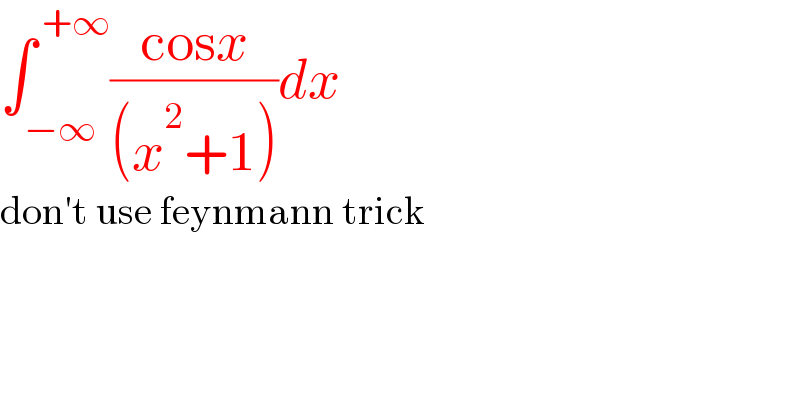
$$\int_{−\infty} ^{\:+\infty} \frac{\mathrm{cos}{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$$$\mathrm{don}'\mathrm{t}\:\mathrm{use}\:\mathrm{feynmann}\:\mathrm{trick} \\ $$
Answered by Ñï= last updated on 12/Apr/21
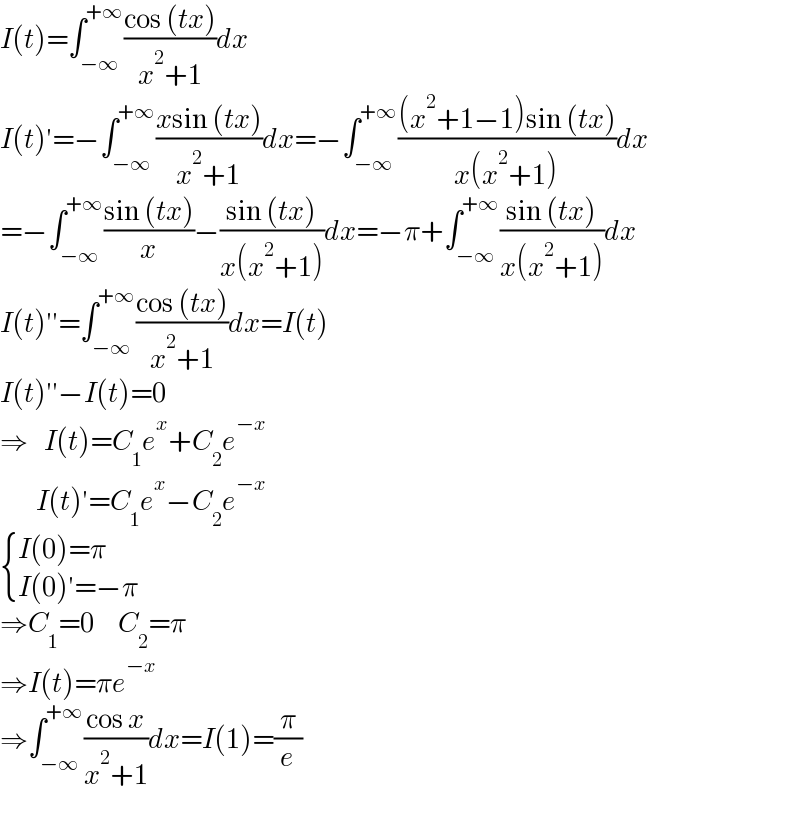
$${I}\left({t}\right)=\int_{−\infty} ^{+\infty} \frac{\mathrm{cos}\:\left({tx}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$${I}\left({t}\right)'=−\int_{−\infty} ^{+\infty} \frac{{x}\mathrm{sin}\:\left({tx}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=−\int_{−\infty} ^{+\infty} \frac{\left({x}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}\right)\mathrm{sin}\:\left({tx}\right)}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$$$=−\int_{−\infty} ^{+\infty} \frac{\mathrm{sin}\:\left({tx}\right)}{{x}}−\frac{\mathrm{sin}\:\left({tx}\right)}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}=−\pi+\int_{−\infty} ^{+\infty} \frac{\mathrm{sin}\:\left({tx}\right)}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$$${I}\left({t}\right)''=\int_{−\infty} ^{+\infty} \frac{\mathrm{cos}\:\left({tx}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}={I}\left({t}\right) \\ $$$${I}\left({t}\right)''−{I}\left({t}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:{I}\left({t}\right)={C}_{\mathrm{1}} {e}^{{x}} +{C}_{\mathrm{2}} {e}^{−{x}} \\ $$$$\:\:\:\:\:\:\:\:\:{I}\left({t}\right)'={C}_{\mathrm{1}} {e}^{{x}} −{C}_{\mathrm{2}} {e}^{−{x}} \\ $$$$\begin{cases}{{I}\left(\mathrm{0}\right)=\pi}\\{{I}\left(\mathrm{0}\right)'=−\pi}\end{cases} \\ $$$$\Rightarrow{C}_{\mathrm{1}} =\mathrm{0}\:\:\:\:\:\:{C}_{\mathrm{2}} =\pi \\ $$$$\Rightarrow{I}\left({t}\right)=\pi{e}^{−{x}} \\ $$$$\Rightarrow\int_{−\infty} ^{+\infty} \frac{\mathrm{cos}\:{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}={I}\left(\mathrm{1}\right)=\frac{\pi}{{e}} \\ $$
Answered by Ñï= last updated on 12/Apr/21
![I=∫_(−∞) ^(+∞) ((cos x)/(x^2 +1))dx=ℜ∫_(−∞) ^(+∞) (e^(ix) /(x^2 +1))dx=ℜ[2πiRes((e^(ix) /(x^2 +1)),i)] =ℜ[2πilim_(x→i) ((x−i)/(x^2 +1))e^(ix) ]=ℜ[2πi∙(e^(−1) /(2i))]=(π/e)](https://www.tinkutara.com/question/Q138325.png)
$${I}=\int_{−\infty} ^{+\infty} \frac{\mathrm{co}{s}\:{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\Re\int_{−\infty} ^{+\infty} \frac{{e}^{{ix}} }{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\Re\left[\mathrm{2}\pi{iRes}\left(\frac{{e}^{{ix}} }{{x}^{\mathrm{2}} +\mathrm{1}},{i}\right)\right] \\ $$$$=\Re\left[\mathrm{2}\pi{i}\underset{{x}\rightarrow{i}} {\mathrm{lim}}\frac{{x}−{i}}{{x}^{\mathrm{2}} +\mathrm{1}}{e}^{{ix}} \right]=\Re\left[\mathrm{2}\pi{i}\centerdot\frac{{e}^{−\mathrm{1}} }{\mathrm{2}{i}}\right]=\frac{\pi}{{e}} \\ $$
Answered by Ñï= last updated on 12/Apr/21
![I(t)=∫_0 ^(+∞) ((cos (tx))/(x^2 +1))dx L[I(t)]=∫_0 ^∞ dx∫_0 ^(+∞) ((cos (tx))/(x^2 +1))e^(−st) dt =∫_0 ^∞ ((L[cos (tx)(s)])/(x^2 +1))dx =∫_0 ^∞ (s/(s^2 +x^2 ))∙(dx/(x^2 +1)) =(s/(s^2 −1))[∫_0 ^∞ (dx/(x^2 +1))dx−∫_0 ^∞ ((sdx)/(x^2 +s^2 ))] =((πs)/(2(s^2 −1)))−(π/(2(s^2 −1))) I(t)=L^(−1) [((πs)/(2(s^2 −1)))−(π/(2(s^2 −1)))] =(π/2)L^(−1) {(s/(s^2 −1))}−(π/2)L^(−1) {(1/(s^2 −1))} =(π/2)(cosh t−sinh t) =(π/2)e^(−t) ⇒∫_(−∞) ^(+∞) ((cos x)/(x^2 +1))dx=2I(1)=(π/e)](https://www.tinkutara.com/question/Q138327.png)
$${I}\left({t}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{cos}\:\left({tx}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\mathcal{L}\left[{I}\left({t}\right)\right]=\int_{\mathrm{0}} ^{\infty} {dx}\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{cos}\:\left({tx}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{e}^{−{st}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathcal{L}\left[\mathrm{cos}\:\left({tx}\right)\left({s}\right)\right]}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{s}}{{s}^{\mathrm{2}} +{x}^{\mathrm{2}} }\centerdot\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{{s}}{{s}^{\mathrm{2}} −\mathrm{1}}\left[\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}−\int_{\mathrm{0}} ^{\infty} \frac{{sdx}}{{x}^{\mathrm{2}} +{s}^{\mathrm{2}} }\right] \\ $$$$=\frac{\pi{s}}{\mathrm{2}\left({s}^{\mathrm{2}} −\mathrm{1}\right)}−\frac{\pi}{\mathrm{2}\left({s}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$${I}\left({t}\right)=\mathcal{L}^{−\mathrm{1}} \left[\frac{\pi{s}}{\mathrm{2}\left({s}^{\mathrm{2}} −\mathrm{1}\right)}−\frac{\pi}{\mathrm{2}\left({s}^{\mathrm{2}} −\mathrm{1}\right)}\right] \\ $$$$=\frac{\pi}{\mathrm{2}}\mathcal{L}^{−\mathrm{1}} \left\{\frac{{s}}{{s}^{\mathrm{2}} −\mathrm{1}}\right\}−\frac{\pi}{\mathrm{2}}\mathcal{L}^{−\mathrm{1}} \left\{\frac{\mathrm{1}}{{s}^{\mathrm{2}} −\mathrm{1}}\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\left(\mathrm{cosh}\:{t}−\mathrm{sinh}\:{t}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}{e}^{−{t}} \\ $$$$\Rightarrow\int_{−\infty} ^{+\infty} \frac{\mathrm{cos}\:{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\mathrm{2}{I}\left(\mathrm{1}\right)=\frac{\pi}{{e}} \\ $$
