Question Number 140988 by mohammad17 last updated on 14/May/21
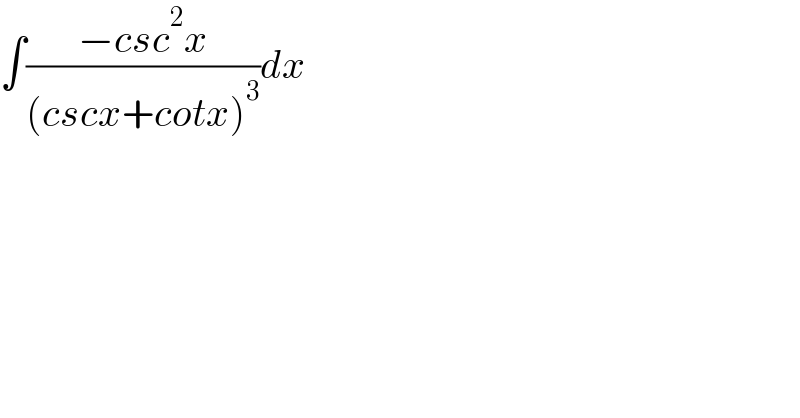
$$\int\frac{−{csc}^{\mathrm{2}} {x}}{\left({cscx}+{cotx}\right)^{\mathrm{3}} }{dx} \\ $$
Answered by MJS_new last updated on 14/May/21
![∫((−csc^2 x)/((csc x +cot x)))dx= [t=cos x → dx=−(dt/(sin x))] =∫(dt/((t+1)^3 ))=−(1/(2(t+1)^2 ))=−(1/(2(1+cos x)^2 ))+C](https://www.tinkutara.com/question/Q140999.png)
$$\int\frac{−\mathrm{csc}^{\mathrm{2}} \:{x}}{\left(\mathrm{csc}\:{x}\:+\mathrm{cot}\:{x}\right)}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{cos}\:{x}\:\rightarrow\:{dx}=−\frac{{dt}}{\mathrm{sin}\:{x}}\right] \\ $$$$=\int\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{3}} }=−\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }+{C} \\ $$
