Question Number 250 by 123456 last updated on 25/Jan/15
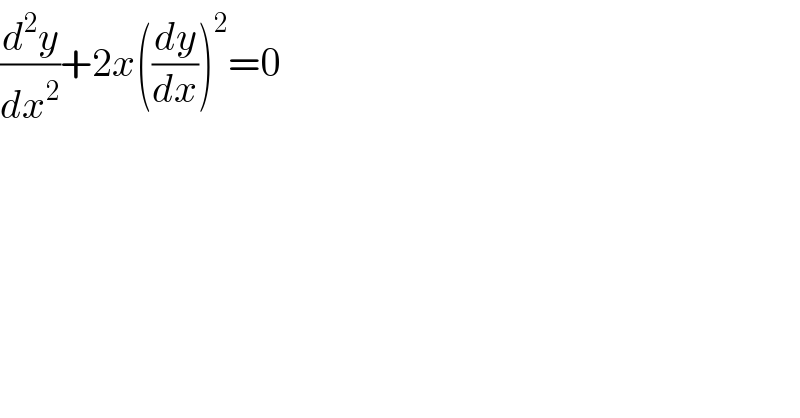
$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{2}{x}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$
Answered by prakash jain last updated on 17/Dec/14

$$\frac{{dy}}{{dx}}={u} \\ $$$$\frac{{du}}{{dx}}+\mathrm{2}{xu}^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{{du}}{{u}^{\mathrm{2}} }=−\mathrm{2}{xdx} \\ $$$$−\frac{\mathrm{1}}{{u}}=−{x}^{\mathrm{2}} +{C} \\ $$$${u}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{C}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{C}} \\ $$$${y}=−\frac{\mathrm{arctanh}\left(\frac{{x}}{\:\sqrt{{C}}}\right)}{\:\sqrt{{C}}}+{C}_{\mathrm{1}} \\ $$
