Question Number 10480 by ssparasmani@gmail.com last updated on 13/Feb/17
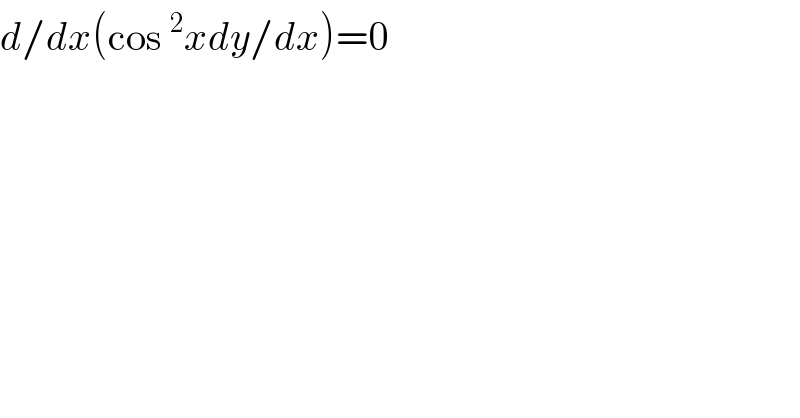
$${d}/{dx}\left(\mathrm{cos}\:^{\mathrm{2}} {xdy}/{dx}\right)=\mathrm{0} \\ $$$$ \\ $$
Answered by mrW1 last updated on 13/Feb/17
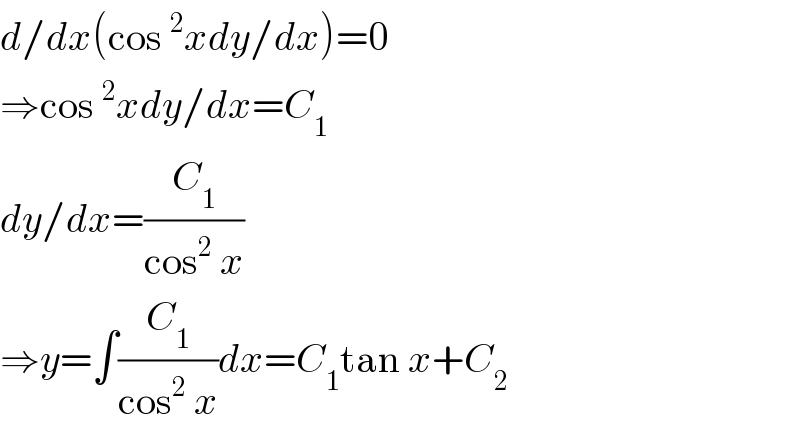
$${d}/{dx}\left(\mathrm{cos}\:^{\mathrm{2}} {xdy}/{dx}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{2}} {xdy}/{dx}={C}_{\mathrm{1}} \\ $$$${dy}/{dx}=\frac{{C}_{\mathrm{1}} }{\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$$$\Rightarrow{y}=\int\frac{{C}_{\mathrm{1}} }{\mathrm{cos}^{\mathrm{2}} \:{x}}{dx}={C}_{\mathrm{1}} \mathrm{tan}\:{x}+{C}_{\mathrm{2}} \\ $$
Answered by robocop last updated on 14/Feb/17
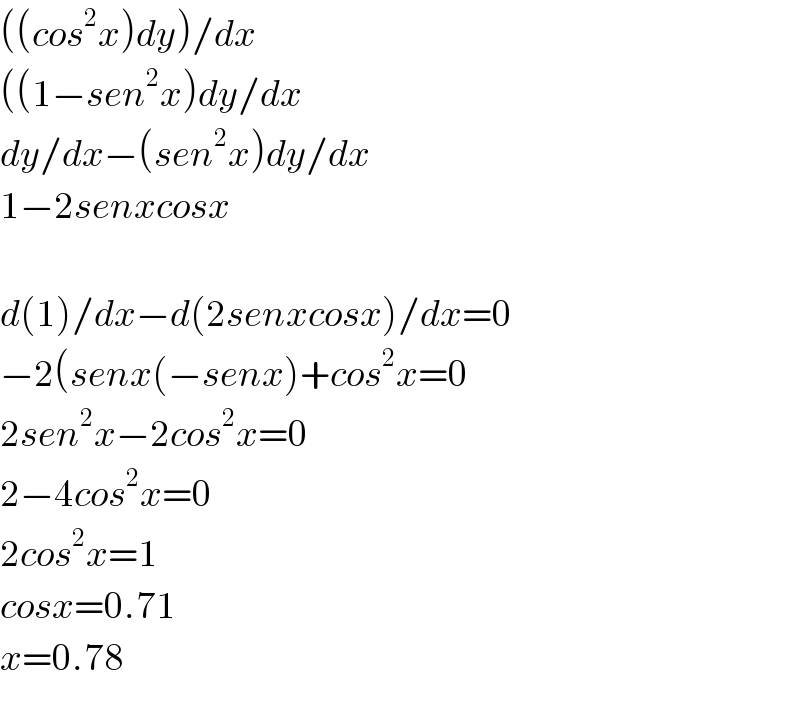
$$\left(\left({cos}^{\mathrm{2}} {x}\right){dy}\right)/{dx} \\ $$$$\left(\left(\mathrm{1}−{sen}^{\mathrm{2}} {x}\right){dy}/{dx}\right. \\ $$$${dy}/{dx}−\left({sen}^{\mathrm{2}} {x}\right){dy}/{dx} \\ $$$$\mathrm{1}−\mathrm{2}{senxcosx} \\ $$$$ \\ $$$${d}\left(\mathrm{1}\right)/{dx}−{d}\left(\mathrm{2}{senxcosx}\right)/{dx}=\mathrm{0} \\ $$$$−\mathrm{2}\left({senx}\left(−{senx}\right)+{cos}^{\mathrm{2}} {x}=\mathrm{0}\right. \\ $$$$\mathrm{2}{sen}^{\mathrm{2}} {x}−\mathrm{2}{cos}^{\mathrm{2}} {x}=\mathrm{0} \\ $$$$\mathrm{2}−\mathrm{4}{cos}^{\mathrm{2}} {x}=\mathrm{0} \\ $$$$\mathrm{2}{cos}^{\mathrm{2}} {x}=\mathrm{1} \\ $$$${cosx}=\mathrm{0}.\mathrm{71} \\ $$$${x}=\mathrm{0}.\mathrm{78} \\ $$
