dear-sir-W-Mjs-the-set-1-4-n-have-the-condition-that-if-two-different-elements-are-selected-and-2112-is-added-to-the-result-then-the-result-is-a-perfect-square-if-n-is-a-positif-number-then

Tinku Tara June 3, 2023 Algebra 0 Comments

Facebook Tweet Pin

Question Number 78399 by john santu last updated on 17/Jan/20

dear sir W, Mjs the set {1,4,n} have the condition that if two different elements are selected and 2112 is added to the result , then the result is a perfect square if n is a positif number . then the number of possible values of n is (A) 8 (B) 7 (C) 6 (D) 5 (E) 4

d e a r s i r W, M j s

t h e s e t {1, 4, n} h a v e t h e c o n d i t i o n t h a t

i f t w o d i f f e r e n t e l e m e n t s a r e

s e l e c t e d a n d 2112 i s a d d e d t o

t h e r e s u l t, t h e n t h e r e s u l t

i s a p e r f e c t s q u a r e i f n i s a

p o s i t i f n u m b e r . t h e n t h e n u m b e r

o f p o s s i b l e v a l u e s o f n i s

(A) 8 (B) 7 (C) 6 (D) 5

(E) 4

Commented by mr W last updated on 17/Jan/20

question is not clear! what means “two different elements are selectet and 2112 is added to the result” when two different elements are selected, say 1 and 4, what is the result? the sum of these two elements or the product of these elements or something else? please make the question clear.

q u e s t i o n i s n o t c l e a r!

w h a t m e a n s “ t w o d i f f e r e n t e l e m e n t s

a r e s e l e c t e t a n d 2112 i s a d d e d t o t h e

{r e s u l t}^{″} w h e n t w o d i f f e r e n t e l e m e n t s

a r e s e l e c t e d, s a y 1 a n d 4, w h a t i s t h e

r e s u l t ? t h e s u m o f t h e s e t w o e l e m e n t s

o r t h e p r o d u c t o f t h e s e e l e m e n t s o r

s o m e t h i n g e l s e ?

p l e a s e m a k e t h e q u e s t i o n c l e a r .

Commented by john santu last updated on 17/Jan/20

the purpose of this problem is if 2 members are selected from the set for example 1 and n then 1×n + 2112 the result are quadratic number

t h e p u r p o s e o f t h i s p r o b l e m

i s i f 2 m e m b e r s a r e s e l e c t e d

f r o m t h e s e t f o r e x a m p l e

1 a n d n t h e n 1 \times n + 2112 t h e

r e s u l t a r e q u a d r a t i c n u m b e r

Commented by mr W last updated on 17/Jan/20

now clear! so the question should be ... if two different elements are selected and 2112 is added to their product , then the result ...

n o w c l e a r! s o t h e q u e s t i o n s h o u l d b e

\dots

i f t w o d i f f e r e n t e l e m e n t s a r e

s e l e c t e d a n d 2112 i s a d d e d t o

t h e i r p r o d u c t, t h e n t h e r e s u l t

\dots

Commented by john santu last updated on 17/Jan/20

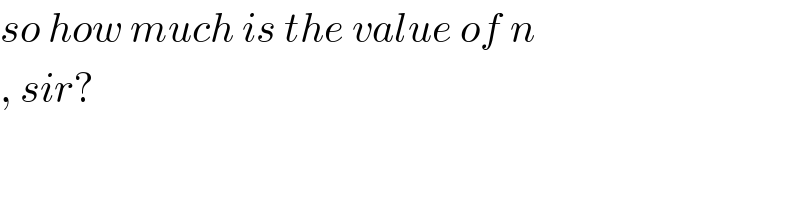
so how much is the value of n , sir?

s o h o w m u c h i s t h e v a l u e o f n

, s i r ?

Commented by john santu last updated on 17/Jan/20

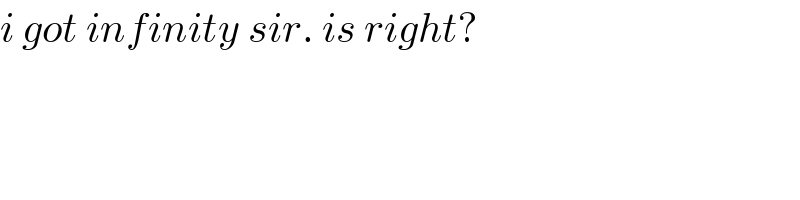
i got infinity sir. is right?

i g o t i n f i n i t y s i r . i s r i g h t ?

Commented by MJS last updated on 17/Jan/20

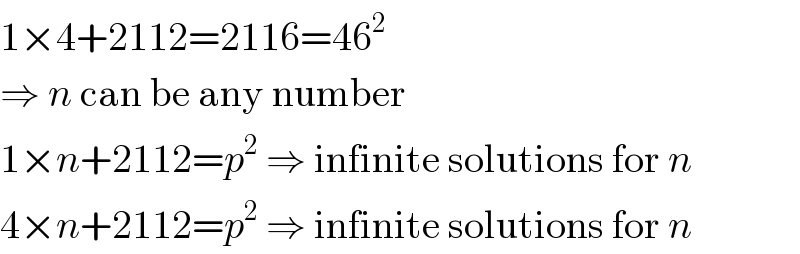
1×4+2112=2116=46^2 ⇒ n can be any number 1×n+2112=p^2 ⇒ infinite solutions for n 4×n+2112=p^2 ⇒ infinite solutions for n

1 \times 4 + 2112 = 2116 = 46^{2}

\Rightarrow n can be any number

1 \times n + 2112 = p^{2} \Rightarrow infinite solutions for n

4 \times n + 2112 = p^{2} \Rightarrow infinite solutions for n

Commented by john santu last updated on 17/Jan/20

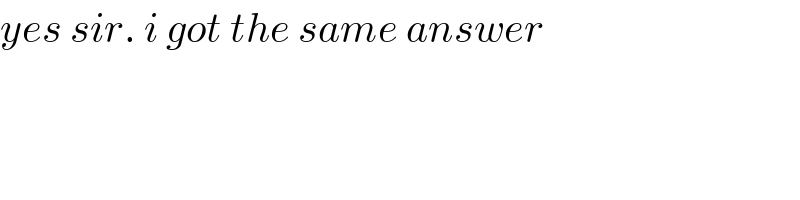
yes sir. i got the same answer

y e s s i r . i g o t t h e s a m e a n s w e r

Commented by mr W last updated on 17/Jan/20

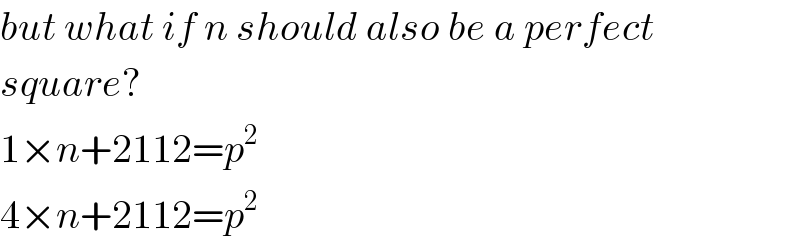
but what if n should also be a perfect square? 1×n+2112=p^2 4×n+2112=p^2

b u t w h a t i f n s h o u l d a l s o b e a p e r f e c t

s q u a r e ?

1 \times n + 2112 = p^{2}

4 \times n + 2112 = p^{2}

Commented by john santu last updated on 17/Jan/20

n is positive number sir

n i s p o s i t i v e n u m b e r s i r

Commented by mr W last updated on 17/Jan/20

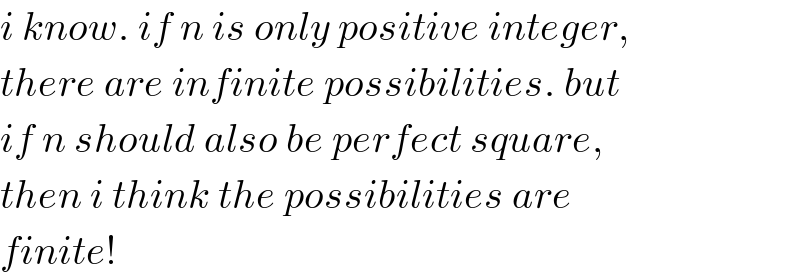
i know. if n is only positive integer, there are infinite possibilities. but if n should also be perfect square, then i think the possibilities are finite!

i k n o w . i f n i s o n l y p o s i t i v e i n t e g e r,

t h e r e a r e i n f i n i t e p o s s i b i l i t i e s . b u t

i f n s h o u l d a l s o b e p e r f e c t s q u a r e,

t h e n i t h i n k t h e p o s s i b i l i t i e s a r e

f i n i t e!

Commented by MJS last updated on 17/Jan/20

let n=(p−q)^2 (1) (p−q)^2 +2112=p^2 ⇒ p=((q^2 +2112)/(2q)) p, q∈N∧0<q≤p ⇒ 0<q≤45 ⇒ q∈{2, 4, 6, 8, 12, 16, 22, 24, 32, 44} p∈{529, 266, 179, 136, 94, 74, 59, 56, 49, 46} n∈{277729, 68644, 29929, 16384, 6724, 3364, 1369, 1024, 289, 4} (2) 4(p−q)^2 +2112=p^2 ⇒ q=p−((√(p^2 −2112))/2) ⇒ p∈{46, 56, 74, 94, 136, 266} q∈{45, 40, 45, 53, 72, 135} n∈{17161, 4096, 1681, 841, 256, 1} still infinite possibilities for n with 1×4+2112=46^2

let n = {(p - q)}^{2}

(1) {(p - q)}^{2} + 2112 = p^{2} \Rightarrow p = \frac{q^{2} + 2112}{2 q}

p, q \in N \land 0 < q ⩽ p \Rightarrow 0 < q ⩽ 45

\Rightarrow

q \in {2, 4, 6, 8, 12, 16, 22, 24, 32, 44}

p \in {529, 266, 179, 136, 94, 74, 59, 56, 49, 46}

n \in {277729, 68644, 29929, 16384, 6724, 3364, 1369, 1024, 289, 4}

(2) 4 {(p - q)}^{2} + 2112 = p^{2} \Rightarrow q = p - \frac{\sqrt{p^{2} - 2112}}{2}

\Rightarrow

p \in {46, 56, 74, 94, 136, 266}

q \in {45, 40, 45, 53, 72, 135}

n \in {17161, 4096, 1681, 841, 256, 1}

still infinite possibilities for n with

1 \times 4 + 2112 = 46^{2}

Commented by Rasheed.Sindhi last updated on 17/Jan/20

n should be such that (1×n+2112) & (4×n+2112) both are perfect squares.

n s h o u l d b e s u c h t h a t

(1 \times n + 2112) & (4 \times n + 2112)

b o t h a r e p e r f e c t s q u a r e s .

Commented by john santu last updated on 17/Jan/20

yes sir. what is value of n possible?

y e s s i r . w h a t i s v a l u e o f n p o s s i b l e ?

Commented by john santu last updated on 17/Jan/20

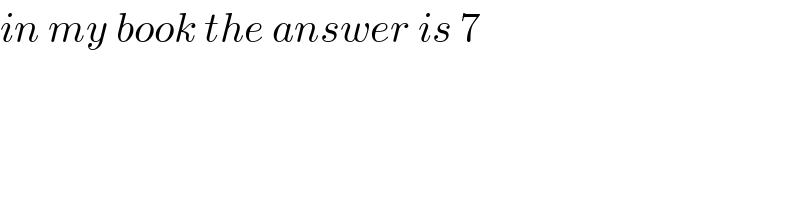
in my book the answer is 7

i n m y b o o k t h e a n s w e r i s 7

Answered by john santu last updated on 17/Jan/20

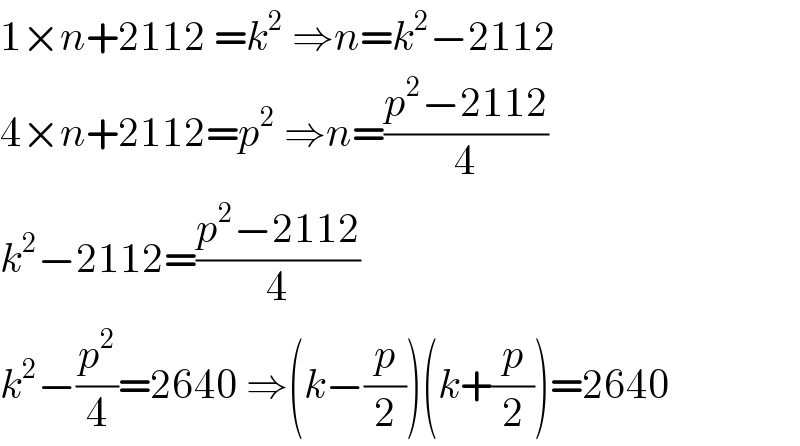
1×n+2112 =k^2 ⇒n=k^2 −2112 4×n+2112=p^2 ⇒n=((p^2 −2112)/4) k^2 −2112=((p^2 −2112)/4) k^2 −(p^2 /4)=2640 ⇒(k−(p/2))(k+(p/2))=2640

1 \times n + 2112 = k^{2} \Rightarrow n = k^{2} - 2112

4 \times n + 2112 = p^{2} \Rightarrow n = \frac{p^{2} - 2112}{4}

k^{2} - 2112 = \frac{p^{2} - 2112}{4}

k^{2} - \frac{p^{2}}{4} = 2640 \Rightarrow (k - \frac{p}{2}) (k + \frac{p}{2}) = 2640

Commented by Rasheed.Sindhi last updated on 17/Jan/20

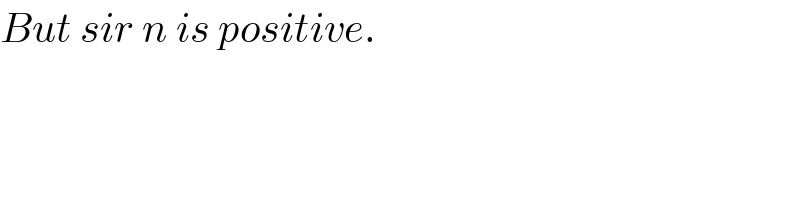
But sir n is positive.

B u t s i r n i s p o s i t i v e .

Commented by MJS last updated on 17/Jan/20

yes. I posted all 9 solutions, then I wrote the last 2 lines...

yes . I posted a l l 9 solutions, then I wrote the

last 2 lines \dots

Commented by MJS last updated on 17/Jan/20

error in last line k^2 −(p^2 /4)=1584 your idea is good, it leads to n∈{−512, −87, 97, 697, 3072, 8497, 16113, 37888, 155497} since we′re looking for n∈N we have indeed 7 solutions

error in last line

k^{2} - \frac{p^{2}}{4} = 1584

your idea is good, it leads to

n \in {- 512, - 87, 97, 697, 3072, 8497, 16113, 37888, 155497}

since {we}^{'} re looking for n \in N we have indeed

7 solutions

Commented by john santu last updated on 17/Jan/20

waw..thanks you sir

w a w . . t h a n k s y o u s i r

Answered by Rasheed.Sindhi last updated on 17/Jan/20

⇒ { ((1×4+2112=46^2 )),((1×n+2112 is perfect square)),((4×n+2112 is perfect square)) :} 4×n+2112 is perfect square ⇒n+528 is perfect square ⇒ { ((n+2112 is perfect square)),((n+528 is perfect square)) :} Let n+528=q^2 n+2112=n+528+1584=p^2 >q^2 q^2 +1584=p^2 (p+q)(p−q)=1584=2^4 .3^2 .11 p,q∈Z^+ ∧ p>q⇒p+q>p−q •For p,q being whole numbers p+q and p−q are both even. p+q=44⇒p−q=36 p+q=48⇒p−q=33 (rejected) p+q=66⇒p−q=24 p+q=88⇒p−q=18 Continue

\Rightarrow {\begin{cases} 1 \times 4 + 2112 = 46^{2} \\ 1 \times n + 2112 i s p e r f e c t s q u a r e \\ 4 \times n + 2112 i s p e r f e c t s q u a r e \end{cases}

4 \times n + 2112 i s p e r f e c t s q u a r e

\Rightarrow n + 528 i s p e r f e c t s q u a r e

\Rightarrow {\begin{cases} n + 2112 i s p e r f e c t s q u a r e \\ n + 528 i s p e r f e c t s q u a r e \end{cases}

L e t n + 528 = q^{2}

n + 2112 = n + 528 + 1584 = p^{2} > q^{2}

q^{2} + 1584 = p^{2}

(p + q) (p - q) = 1584 = 2^{4} . 3^{2} . 11

p, q \in Z^{+} \land p > q \Rightarrow p + q > p - q

∙ F o r p, q b e i n g w h o l e n u m b e r s

p + q a n d p - q a r e b o t h e v e n .

p + q = 44 \Rightarrow p - q = 36

p + q = 48 \Rightarrow p - q = 33 (r e j e c t e d)

p + q = 66 \Rightarrow p - q = 24

p + q = 88 \Rightarrow p - q = 18

C o n t i n u e

Commented by john santu last updated on 17/Jan/20

thanks you

t h a n k s y o u

t h a n k s y o u

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Facebook Tweet Pin

Leave a Reply Cancel reply