Menu Close

Determine-1-a-r-ar-a-2r-ar-2-a-n-1-r-ar-n-1-

Tinku Tara 0 Comments
Pin




Question Number 5784 by Rasheed Soomro last updated on 27/May/16
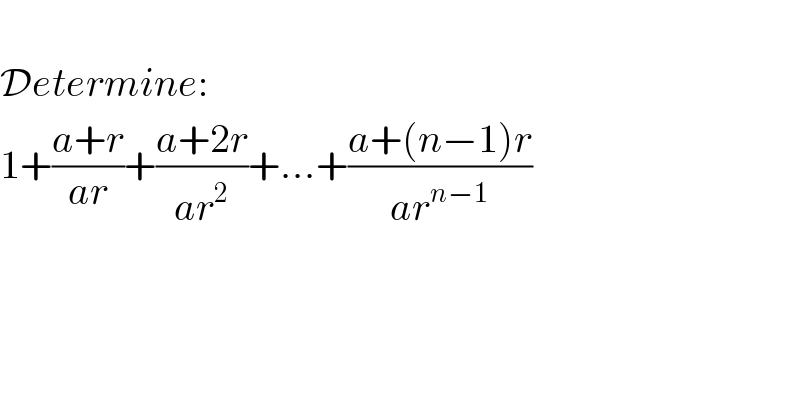
Determine: 1+((a+r)/(ar))+((a+2r)/(ar^2 ))+...+((a+(n−1)r)/(ar^(n−1) ))
$$ \\ $$$$\mathcal{D}{etermine}: \\ $$$$\mathrm{1}+\frac{{a}+{r}}{{ar}}+\frac{{a}+\mathrm{2}{r}}{{ar}^{\mathrm{2}} }+…+\frac{{a}+\left({n}−\mathrm{1}\right){r}}{{ar}^{{n}−\mathrm{1}} } \\ $$
Answered by Yozzii last updated on 27/May/16
S(n)=1+((a+r)/(ar))+((a+2r)/(ar^2 ))+((a+3r)/(ar^3 ))+...+((a+(n−3)r)/(ar^(n−3) ))+((a+(n−2)r)/(ar^(n−2) ))+((a+(n−1)r)/(ar^(n−1) )) S(n)=1+((1/r)+(1/a))+((1/r^2 )+(2/(ar)))+((1/r^3 )+(3/(ar^2 )))+((1/r^4 )+(4/(ar^3 )))+((1/r^5 )+(5/(ar^4 )))+...+((1/r^(n−3) )+((n−3)/(ar^(n−4) )))+((1/r^(n−2) )+((n−2)/(ar^(n−3) )))+((1/r^(n−1) )+((n−1)/(ar^(n−2) ))) ⇒rS(n)=r+(1+(r/a))+((1/r)+(2/a))+((1/r^2 )+(3/(ar)))+((1/r^3 )+(4/(ar^2 )))+((1/r^4 )+(5/(ar^3 )))+...+((1/r^(n−4) )+((n−3)/(ar^(n−5) )))+((1/r^(n−3) )+((n−2)/(ar^(n−4) )))+((1/r^(n−2) )+((n−1)/(ar^(n−3) ))) ⇒(1−r)S(n)=−r−(2/a)+1−1+(1/r)−(1/r)+(1/a)−(r/a)+(1/r^2 )−(1/r^2 )+(2/(ar))−(3/(ar))+(1/r^3 )−(1/r^3 )+(3/(ar^2 ))−(4/(ar^2 ))+(1/r^4 )−(1/r^4 )+(4/(ar^3 ))−(5/(ar^3 ))+...+(1/r^(n−3) )−(1/r^(n−3) )−(1/(ar^(n−4) ))+0−(1/(ar^(n−3) ))+(1/r^(n−1) )+((n−1)/(ar^(n−2) )) (1−r)S(n)=−r−((1+r)/a)−((1/(ar))+(1/(ar^2 ))+(1/(ar^3 ))+...+(1/(ar^(n−4) ))+(1/(ar^(n−3) ))+(1/(ar^(n−2) )))+(1/r^(n−1) )+(n/(ar^(n−2) )) (1−r)S(n)=−((1+r)/a)+(1/r^(n−1) )+(n/(ar^(n−2) ))−r−(1/(ar))(1+(1/r)+(1/r^2 )+...(1/r^(n−5) )+(1/r^(n−4) )+(1/r^(n−3) )) S(n)=(1/(1−r))(−((1+r)/a)+(1/r^(n−1) )+(n/(ar^(n−2) ))−r−(1/(ar))(((1−(1/r^(n−2) ))/(1−(1/r))))) S(n)=(1/(r−1))(r+((r+1)/a)+(1/(ar))((((r^(n−2) −1)/r^(n−2) )/((r−1)/r)))−(1/r^(n−1) )−(n/(ar^(n−2) ))) S(n)=(1/(r−1))(r+((r+1)/a)+((r^(n−2) −1)/(ar^(n−2) (r−1)))−(1/r^(n−1) )−(n/(ar^(n−2) ))) −−−−−−−−−−−−−−−−−−−−−−−−−− E.g. n=1 S(1)=(1/(r−1))(r+((r+1)/a)+((r^(−1) −1)/(ar^(−1) (r−1)))−1−(1/(ar^(−1) ))) S(1)=(1/(r−1))(r−1+((r+1)/a)+((r^(−1) −1)/(a(1−r^(−1) )))−(r/a)) S(1)=(1/(r−1))(r−1+(1/a)−(1/a)) S(1)=((r−1)/(r−1))=1 (r≠1) n=2 S(2)=(1/(r−1))(r+(r/a)+(1/a)+0−(1/r)−(2/a)) S(2)=(1/(r−1))(((r^2 −1)/r)+((r−1)/a)) S(2)=((r+1)/r)+(1/a)=1+(1/r)+(1/a)=1+((a+r)/(ar))
$${S}\left({n}\right)=\mathrm{1}+\frac{{a}+{r}}{{ar}}+\frac{{a}+\mathrm{2}{r}}{{ar}^{\mathrm{2}} }+\frac{{a}+\mathrm{3}{r}}{{ar}^{\mathrm{3}} }+…+\frac{{a}+\left({n}−\mathrm{3}\right){r}}{{ar}^{{n}−\mathrm{3}} }+\frac{{a}+\left({n}−\mathrm{2}\right){r}}{{ar}^{{n}−\mathrm{2}} }+\frac{{a}+\left({n}−\mathrm{1}\right){r}}{{ar}^{{n}−\mathrm{1}} } \\ $$$${S}\left({n}\right)=\mathrm{1}+\left(\frac{\mathrm{1}}{{r}}+\frac{\mathrm{1}}{{a}}\right)+\left(\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+\frac{\mathrm{2}}{{ar}}\right)+\left(\frac{\mathrm{1}}{{r}^{\mathrm{3}} }+\frac{\mathrm{3}}{{ar}^{\mathrm{2}} }\right)+\left(\frac{\mathrm{1}}{{r}^{\mathrm{4}} }+\frac{\mathrm{4}}{{ar}^{\mathrm{3}} }\right)+\left(\frac{\mathrm{1}}{{r}^{\mathrm{5}} }+\frac{\mathrm{5}}{{ar}^{\mathrm{4}} }\right)+…+\left(\frac{\mathrm{1}}{{r}^{{n}−\mathrm{3}} }+\frac{{n}−\mathrm{3}}{{ar}^{{n}−\mathrm{4}} }\right)+\left(\frac{\mathrm{1}}{{r}^{{n}−\mathrm{2}} }+\frac{{n}−\mathrm{2}}{{ar}^{{n}−\mathrm{3}} }\right)+\left(\frac{\mathrm{1}}{{r}^{{n}−\mathrm{1}} }+\frac{{n}−\mathrm{1}}{{ar}^{{n}−\mathrm{2}} }\right) \\ $$$$\Rightarrow{rS}\left({n}\right)={r}+\left(\mathrm{1}+\frac{{r}}{{a}}\right)+\left(\frac{\mathrm{1}}{{r}}+\frac{\mathrm{2}}{{a}}\right)+\left(\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+\frac{\mathrm{3}}{{ar}}\right)+\left(\frac{\mathrm{1}}{{r}^{\mathrm{3}} }+\frac{\mathrm{4}}{{ar}^{\mathrm{2}} }\right)+\left(\frac{\mathrm{1}}{{r}^{\mathrm{4}} }+\frac{\mathrm{5}}{{ar}^{\mathrm{3}} }\right)+…+\left(\frac{\mathrm{1}}{{r}^{{n}−\mathrm{4}} }+\frac{{n}−\mathrm{3}}{{ar}^{{n}−\mathrm{5}} }\right)+\left(\frac{\mathrm{1}}{{r}^{{n}−\mathrm{3}} }+\frac{{n}−\mathrm{2}}{{ar}^{{n}−\mathrm{4}} }\right)+\left(\frac{\mathrm{1}}{{r}^{{n}−\mathrm{2}} }+\frac{{n}−\mathrm{1}}{{ar}^{{n}−\mathrm{3}} }\right) \\ $$$$\Rightarrow\left(\mathrm{1}−{r}\right){S}\left({n}\right)=−{r}−\frac{\mathrm{2}}{{a}}+\mathrm{1}−\mathrm{1}+\frac{\mathrm{1}}{{r}}−\frac{\mathrm{1}}{{r}}+\frac{\mathrm{1}}{{a}}−\frac{{r}}{{a}}+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }−\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+\frac{\mathrm{2}}{{ar}}−\frac{\mathrm{3}}{{ar}}+\frac{\mathrm{1}}{{r}^{\mathrm{3}} }−\frac{\mathrm{1}}{{r}^{\mathrm{3}} }+\frac{\mathrm{3}}{{ar}^{\mathrm{2}} }−\frac{\mathrm{4}}{{ar}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{4}} }−\frac{\mathrm{1}}{{r}^{\mathrm{4}} }+\frac{\mathrm{4}}{{ar}^{\mathrm{3}} }−\frac{\mathrm{5}}{{ar}^{\mathrm{3}} }+…+\frac{\mathrm{1}}{{r}^{{n}−\mathrm{3}} }−\frac{\mathrm{1}}{{r}^{{n}−\mathrm{3}} }−\frac{\mathrm{1}}{{ar}^{{n}−\mathrm{4}} }+\mathrm{0}−\frac{\mathrm{1}}{{ar}^{{n}−\mathrm{3}} }+\frac{\mathrm{1}}{{r}^{{n}−\mathrm{1}} }+\frac{{n}−\mathrm{1}}{{ar}^{{n}−\mathrm{2}} } \\ $$$$\left(\mathrm{1}−{r}\right){S}\left({n}\right)=−{r}−\frac{\mathrm{1}+{r}}{{a}}−\left(\frac{\mathrm{1}}{{ar}}+\frac{\mathrm{1}}{{ar}^{\mathrm{2}} }+\frac{\mathrm{1}}{{ar}^{\mathrm{3}} }+…+\frac{\mathrm{1}}{{ar}^{{n}−\mathrm{4}} }+\frac{\mathrm{1}}{{ar}^{{n}−\mathrm{3}} }+\frac{\mathrm{1}}{{ar}^{{n}−\mathrm{2}} }\right)+\frac{\mathrm{1}}{{r}^{{n}−\mathrm{1}} }+\frac{{n}}{{ar}^{{n}−\mathrm{2}} } \\ $$$$\left(\mathrm{1}−{r}\right){S}\left({n}\right)=−\frac{\mathrm{1}+{r}}{{a}}+\frac{\mathrm{1}}{{r}^{{n}−\mathrm{1}} }+\frac{{n}}{{ar}^{{n}−\mathrm{2}} }−{r}−\frac{\mathrm{1}}{{ar}}\left(\mathrm{1}+\frac{\mathrm{1}}{{r}}+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+…\frac{\mathrm{1}}{{r}^{{n}−\mathrm{5}} }+\frac{\mathrm{1}}{{r}^{{n}−\mathrm{4}} }+\frac{\mathrm{1}}{{r}^{{n}−\mathrm{3}} }\right) \\ $$$${S}\left({n}\right)=\frac{\mathrm{1}}{\mathrm{1}−{r}}\left(−\frac{\mathrm{1}+{r}}{{a}}+\frac{\mathrm{1}}{{r}^{{n}−\mathrm{1}} }+\frac{{n}}{{ar}^{{n}−\mathrm{2}} }−{r}−\frac{\mathrm{1}}{{ar}}\left(\frac{\mathrm{1}−\frac{\mathrm{1}}{{r}^{{n}−\mathrm{2}} }}{\mathrm{1}−\frac{\mathrm{1}}{{r}}}\right)\right) \\ $$$${S}\left({n}\right)=\frac{\mathrm{1}}{{r}−\mathrm{1}}\left({r}+\frac{{r}+\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{ar}}\left(\frac{\left({r}^{{n}−\mathrm{2}} −\mathrm{1}\right)/{r}^{{n}−\mathrm{2}} }{\left({r}−\mathrm{1}\right)/{r}}\right)−\frac{\mathrm{1}}{{r}^{{n}−\mathrm{1}} }−\frac{{n}}{{ar}^{{n}−\mathrm{2}} }\right) \\ $$$${S}\left({n}\right)=\frac{\mathrm{1}}{{r}−\mathrm{1}}\left({r}+\frac{{r}+\mathrm{1}}{{a}}+\frac{{r}^{{n}−\mathrm{2}} −\mathrm{1}}{{ar}^{{n}−\mathrm{2}} \left({r}−\mathrm{1}\right)}−\frac{\mathrm{1}}{{r}^{{n}−\mathrm{1}} }−\frac{{n}}{{ar}^{{n}−\mathrm{2}} }\right) \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${E}.{g}.\:{n}=\mathrm{1} \\ $$$${S}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{{r}−\mathrm{1}}\left({r}+\frac{{r}+\mathrm{1}}{{a}}+\frac{{r}^{−\mathrm{1}} −\mathrm{1}}{{ar}^{−\mathrm{1}} \left({r}−\mathrm{1}\right)}−\mathrm{1}−\frac{\mathrm{1}}{{ar}^{−\mathrm{1}} }\right) \\ $$$${S}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{{r}−\mathrm{1}}\left({r}−\mathrm{1}+\frac{{r}+\mathrm{1}}{{a}}+\frac{{r}^{−\mathrm{1}} −\mathrm{1}}{{a}\left(\mathrm{1}−{r}^{−\mathrm{1}} \right)}−\frac{{r}}{{a}}\right) \\ $$$${S}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{{r}−\mathrm{1}}\left({r}−\mathrm{1}+\frac{\mathrm{1}}{{a}}−\frac{\mathrm{1}}{{a}}\right) \\ $$$${S}\left(\mathrm{1}\right)=\frac{{r}−\mathrm{1}}{{r}−\mathrm{1}}=\mathrm{1}\:\:\left({r}\neq\mathrm{1}\right) \\ $$$${n}=\mathrm{2} \\ $$$${S}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{{r}−\mathrm{1}}\left({r}+\frac{{r}}{{a}}+\frac{\mathrm{1}}{{a}}+\mathrm{0}−\frac{\mathrm{1}}{{r}}−\frac{\mathrm{2}}{{a}}\right) \\ $$$${S}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{{r}−\mathrm{1}}\left(\frac{{r}^{\mathrm{2}} −\mathrm{1}}{{r}}+\frac{{r}−\mathrm{1}}{{a}}\right) \\ $$$${S}\left(\mathrm{2}\right)=\frac{{r}+\mathrm{1}}{{r}}+\frac{\mathrm{1}}{{a}}=\mathrm{1}+\frac{\mathrm{1}}{{r}}+\frac{\mathrm{1}}{{a}}=\mathrm{1}+\frac{{a}+{r}}{{ar}} \\ $$
Commented by Rasheed Soomro last updated on 28/May/16
T_(HANK) S!
$$\mathcal{T}_{\mathcal{HANK}} \mathcal{S}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *