Question Number 2007 by Rasheed Soomro last updated on 29/Oct/15
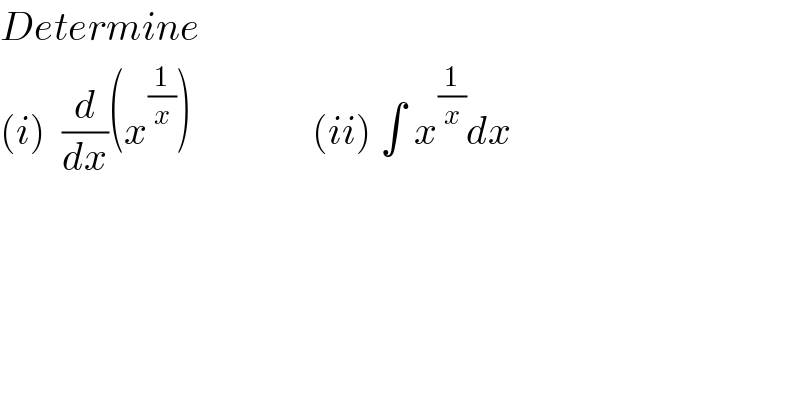
$${Determine} \\ $$$$\left({i}\right)\:\:\frac{{d}}{{dx}}\left({x}^{\frac{\mathrm{1}}{{x}}} \right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({ii}\right)\:\int\:{x}^{\frac{\mathrm{1}}{{x}}} {dx} \\ $$
Answered by Yozzi last updated on 29/Oct/15

$${Let}\:{y}={x}^{\mathrm{1}/{x}} . \\ $$$${If}\:{we}\:{take}\:{logarithms}\:{to}\:{base}\:{e},\:{where} \\ $$$${we}\:{assume}\:{x}>\mathrm{0}\:\left(\Rightarrow{y}>\mathrm{0}\right),\:{we}\:{obtain} \\ $$$${lny}={lnx}^{\mathrm{1}/{x}} \\ $$$$\Rightarrow{lny}=\frac{\mathrm{1}}{{x}}{lnx}\:\:\:\:\left({power}\:{rule}\:{of}\:{logs}\right) \\ $$$${Differentiating}\:{the}\:{equation}\:{implicitly} \\ $$$${w}.{r}.{t}\:\:{x}\:{we}\:{have} \\ $$$$\frac{\mathrm{1}}{{y}}×\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{{x}}×\frac{\mathrm{1}}{{x}}+\frac{−\mathrm{1}}{{x}^{\mathrm{2}} }{lnx}\:\:\: \\ $$$$\Rightarrow\frac{{dy}}{{dx}}={y}\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\mathrm{1}−{lnx}\right) \\ $$$$\therefore\:\frac{{d}}{{dx}}\left({x}^{\mathrm{1}/{x}} \right)={x}^{\mathrm{1}/{x}} ×\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\mathrm{1}−{lnx}\right)={x}^{\frac{\mathrm{1}}{{x}}−\mathrm{2}} \left(\mathrm{1}−{lnx}\right) \\ $$$$\:\:\:\:\:\left({x}>\mathrm{0}\right) \\ $$$${Continue}…\:\left({on}\:{to}\:{the}\:{integral}\:{which}\right. \\ $$$$\left.{looks}\:{difficult}\:{to}\:{find}\right) \\ $$$$\:\:\:\:\: \\ $$$$ \\ $$
