Question Number 2006 by Rasheed Soomro last updated on 29/Oct/15
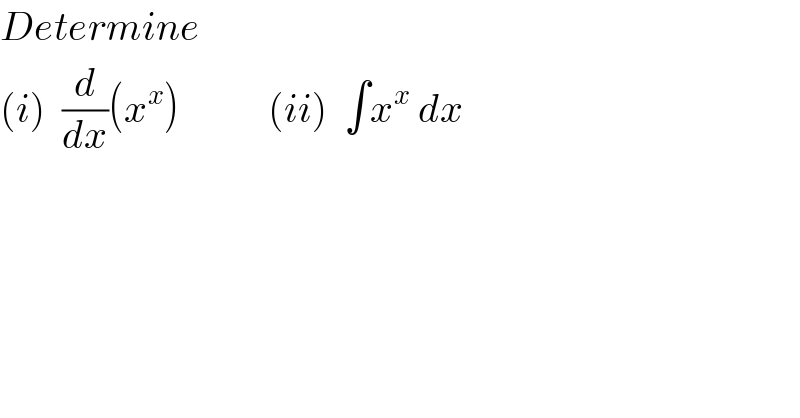
$${Determine} \\ $$$$\left({i}\right)\:\:\frac{{d}}{{dx}}\left({x}^{{x}} \right)\:\:\:\:\:\:\:\:\:\:\:\left({ii}\right)\:\:\int{x}^{{x}} \:{dx} \\ $$
Answered by 123456 last updated on 29/Oct/15
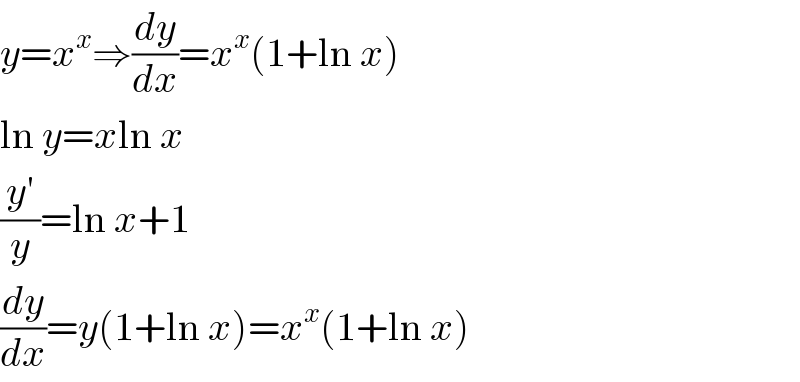
$${y}={x}^{{x}} \Rightarrow\frac{{dy}}{{dx}}={x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right) \\ $$$$\mathrm{ln}\:{y}={x}\mathrm{ln}\:{x} \\ $$$$\frac{{y}'}{{y}}=\mathrm{ln}\:{x}+\mathrm{1} \\ $$$$\frac{{dy}}{{dx}}={y}\left(\mathrm{1}+\mathrm{ln}\:{x}\right)={x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right) \\ $$
