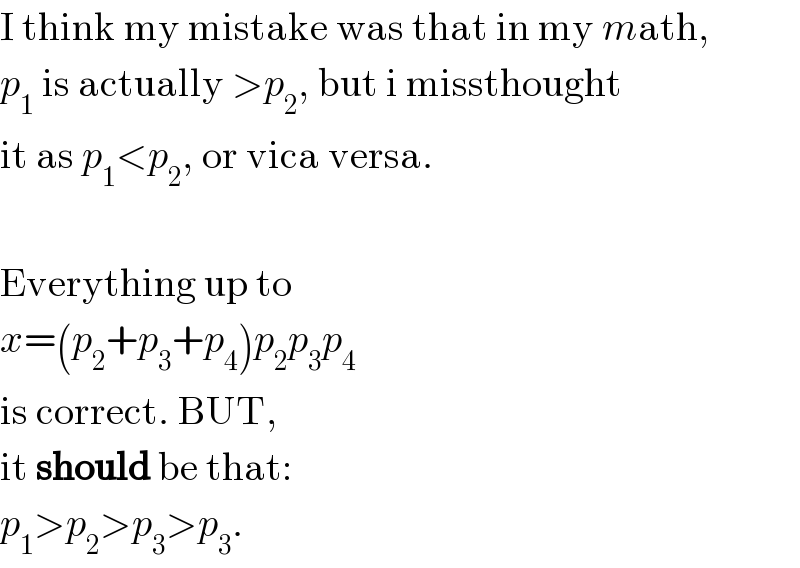Determine-number-s-that-is-are-comprised-of-four-distinct-prime-factors-such-that-difference-of-largest-and-smallest-prime-factors-is-equal-to-the-sum-of-remaining-two-factors-Prop

FacebookTweetPin

Question Number 9025 by Rasheed Soomro last updated on 15/Nov/16

$$\mathrm{Determine}\mathrm{number}/\mathrm{s}\mathrm{that}\mathrm{is}/\mathrm{are}\mathrm{comprised}$$$$\mathrm{of}\mathrm{four}\mathrm{distinct}\mathrm{prime}\mathrm{factors}\mathrm{such}\mathrm{that}$$$$\mathrm{difference}\mathrm{of}\mathrm{largest}\mathrm{and}\mathrm{smallest}\mathrm{prime}$$$$\mathrm{factors}\mathrm{is}\mathrm{equal}\mathrm{to}\mathrm{the}\mathrm{sum}\mathrm{of}\mathrm{remaining}$$$$\mathrm{two}\mathrm{factors}.{}_{\mathrm{Propsed}\mathrm{by}\mathrm{Rasheed}\mathrm{Soomro}}$$

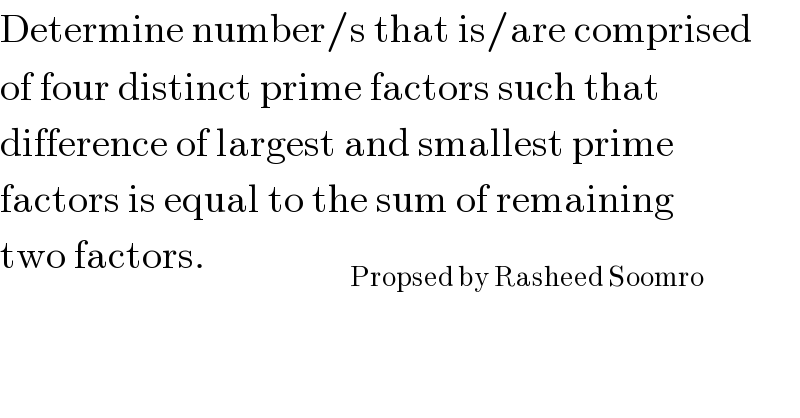
Commented by FilupSmith last updated on 15/Nov/16

$$\mathrm{Do}\mathrm{you}\mathrm{mean}:$$$$n=p_1{p}_2{p}_3{p}_4$$$$p_a>p_{a+1}$$$$p_1-p_4=p_2+p_3$$$$p_a\in \mathbb{P},p_a\ne p_{a+i}\mathrm{\forall }i/\left\{0\right\}$$$$n=?$$

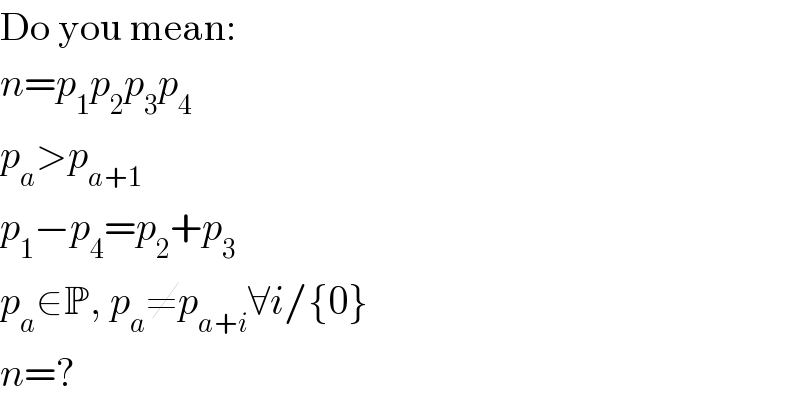
Commented by Rasheed Soomro last updated on 16/Nov/16

$$\mathrm{Yes}\mathrm{Filup}\mathrm{I}\mathrm{mean}\mathrm{that}.$$

Commented by FilupSmith last updated on 16/Nov/16

$$working/playingaround$$$$x=p_1{p}_2{p}_3{p}_4$$$$$$$$p_1-p_4=p_2+p_3$$$$p_1=p_2+p_3+p_4$$$$\therefore x=(p_2+p_3+p_4)p_2{p}_3{p}_4$$$$\therefore p_2+p_3+p_4\in \mathbb{P}$$$$$$$$p_2+p_3+p_4<p_2<p_3<p_4$$$$p_2<p_2-p_3<-p_4<-p_3$$$$$$$$p_2\mathrm{is}+\mathrm{ve}$$$$p_2-p_3\mathrm{is}-\mathrm{ve}$$$$-p_4\mathrm{and}-p_3\mathrm{are}-\mathrm{ve}$$$$$$$$\therefore idontthinksuchnumberexists$$$$astheequalityisnotpossible$$$$working/playingaround$$

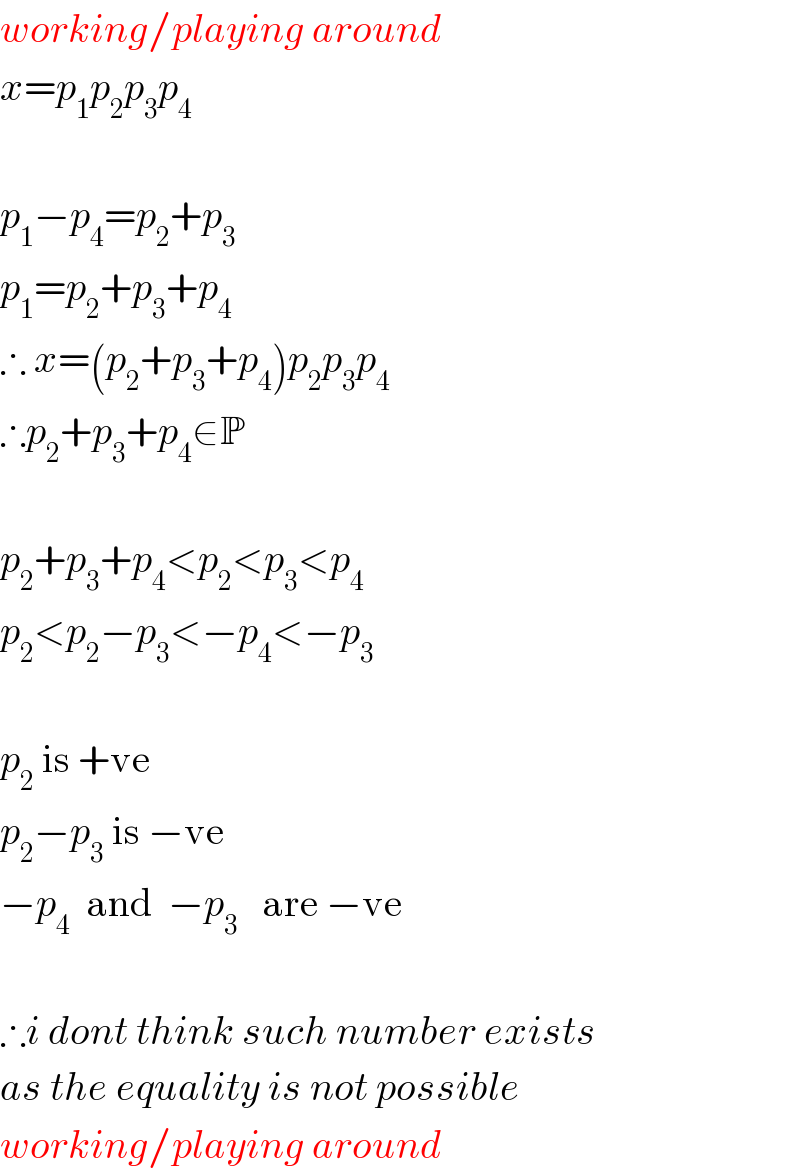
Commented by mrW last updated on 16/Nov/16

$$whenItakealookatthetableof$$$$primenumbersIthinkthere$$$$shouldbeinfinitelymanysuch$$$$numbers,suchas$$$$x=3\times 5\times 11\times 19$$$$x=5\times 7\times 11\times 23$$$$x=3\times 7\times 13\times 23$$$$etc.$$

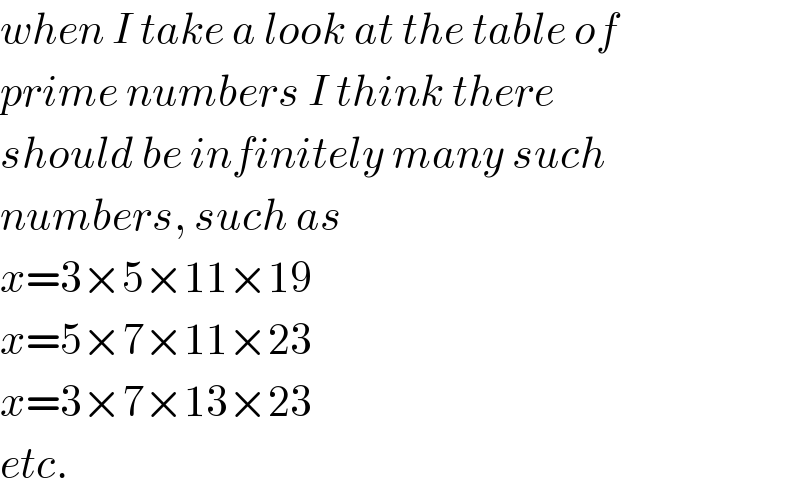
Commented by Rasheed Soomro last updated on 16/Nov/16

$${}^{\bullet }\mathcal{TH}\alpha nksofyouboth!$$$${}^{\bullet }\mathrm{Good}\mathrm{attack}\mathrm{of}\mathrm{Filup}\mathrm{to}\mathrm{the}\mathrm{problem}\mathrm{but}$$$$\mathrm{failed}\mathrm{in}\mathrm{the}\mathrm{end}!$$$${}^{\bullet }\mathrm{I}\mathrm{also}\mathrm{think}\mathrm{that}\mathrm{such}\mathrm{numbers}\mathrm{are}\mathrm{infinite}$$$$\mathrm{but}\mathbf{Can}\mathbf{we}\mathbf{prove}\mathbf{that}\mathbf{such}\mathbf{numbers}\mathbf{are}\mathbf{infimite}?$$$$$$

Commented by FilupSmith last updated on 16/Nov/16

$$\mathrm{I}\mathrm{wonder}\mathrm{where}\mathrm{I}\mathrm{went}\mathrm{wrong}$$

Commented by FilupSmith last updated on 16/Nov/16

$$\mathrm{I}\mathrm{think}\mathrm{my}\mathrm{mistake}\mathrm{was}\mathrm{that}\mathrm{in}\mathrm{my}m\mathrm{ath},$$$$p_1\mathrm{is}\mathrm{actually}>p_2,\mathrm{but}\mathrm{i}\mathrm{missthought}$$$$\mathrm{it}\mathrm{as}{p}_1<p_2,\mathrm{or}\mathrm{vica}\mathrm{versa}.$$$$$$$$\mathrm{Everything}\mathrm{up}\mathrm{to}$$$$x=(p_2+p_3+p_4)p_2{p}_3{p}_4$$$$\mathrm{is}\mathrm{correct}.\mathrm{BUT},$$$$\mathrm{it}\mathbf{should}\mathrm{be}\mathrm{that}:$$$$p_1>p_2>p_3>p_3.$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin