Menu Close

Determine-S-S-a-2-ar-a-r-ar-2-a-2r-ar-n-1-a-n-1-r-

Tinku Tara 0 Comments
Pin




Question Number 5742 by Rasheed Soomro last updated on 26/May/16
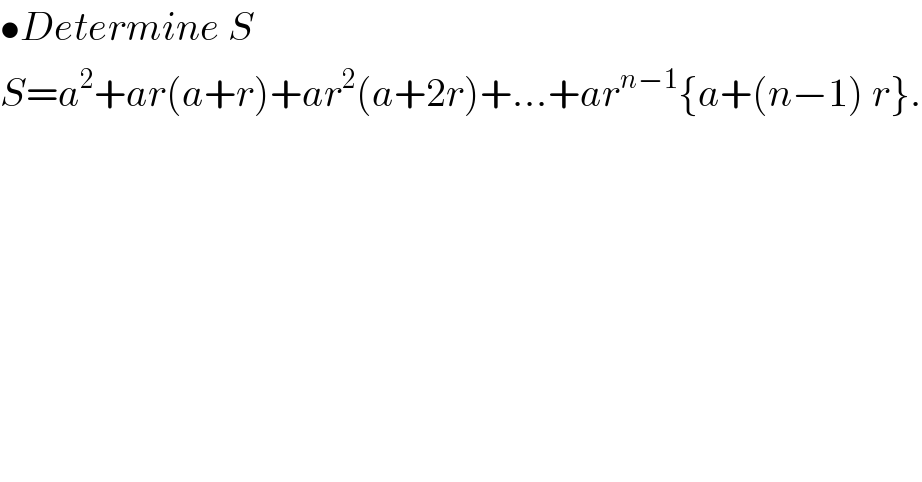
•Determine S S=a^2 +ar(a+r)+ar^2 (a+2r)+...+ar^(n−1) {a+(n−1) r}.
$$\bullet{Determine}\:{S} \\ $$$${S}={a}^{\mathrm{2}} +{ar}\left({a}+{r}\right)+{ar}^{\mathrm{2}} \left({a}+\mathrm{2}{r}\right)+…+{ar}^{{n}−\mathrm{1}} \left\{{a}+\left({n}−\mathrm{1}\right)\:{r}\right\}. \\ $$$$ \\ $$
Answered by Yozzii last updated on 26/May/16
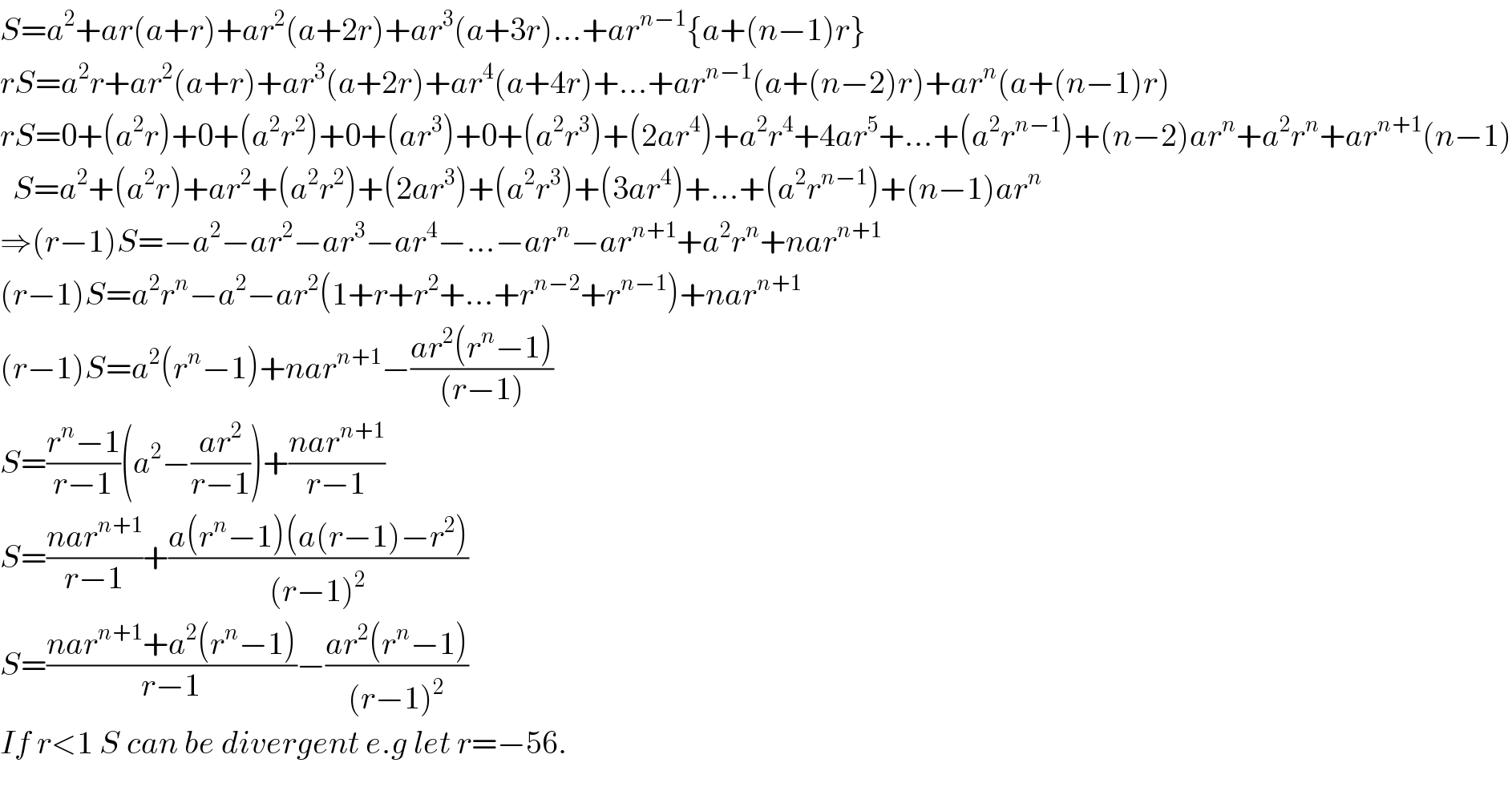
S=a^2 +ar(a+r)+ar^2 (a+2r)+ar^3 (a+3r)...+ar^(n−1) {a+(n−1)r} rS=a^2 r+ar^2 (a+r)+ar^3 (a+2r)+ar^4 (a+4r)+...+ar^(n−1) (a+(n−2)r)+ar^n (a+(n−1)r) rS=0+(a^2 r)+0+(a^2 r^2 )+0+(ar^3 )+0+(a^2 r^3 )+(2ar^4 )+a^2 r^4 +4ar^5 +...+(a^2 r^(n−1) )+(n−2)ar^n +a^2 r^n +ar^(n+1) (n−1) S=a^2 +(a^2 r)+ar^2 +(a^2 r^2 )+(2ar^3 )+(a^2 r^3 )+(3ar^4 )+...+(a^2 r^(n−1) )+(n−1)ar^n ⇒(r−1)S=−a^2 −ar^2 −ar^3 −ar^4 −...−ar^n −ar^(n+1) +a^2 r^n +nar^(n+1) (r−1)S=a^2 r^n −a^2 −ar^2 (1+r+r^2 +...+r^(n−2) +r^(n−1) )+nar^(n+1) (r−1)S=a^2 (r^n −1)+nar^(n+1) −((ar^2 (r^n −1))/((r−1))) S=((r^n −1)/(r−1))(a^2 −((ar^2 )/(r−1)))+((nar^(n+1) )/(r−1)) S=((nar^(n+1) )/(r−1))+((a(r^n −1)(a(r−1)−r^2 ))/((r−1)^2 )) S=((nar^(n+1) +a^2 (r^n −1))/(r−1))−((ar^2 (r^n −1))/((r−1)^2 )) If r<1 S can be divergent e.g let r=−56.
$${S}={a}^{\mathrm{2}} +{ar}\left({a}+{r}\right)+{ar}^{\mathrm{2}} \left({a}+\mathrm{2}{r}\right)+{ar}^{\mathrm{3}} \left({a}+\mathrm{3}{r}\right)…+{ar}^{{n}−\mathrm{1}} \left\{{a}+\left({n}−\mathrm{1}\right){r}\right\} \\ $$$${rS}={a}^{\mathrm{2}} {r}+{ar}^{\mathrm{2}} \left({a}+{r}\right)+{ar}^{\mathrm{3}} \left({a}+\mathrm{2}{r}\right)+{ar}^{\mathrm{4}} \left({a}+\mathrm{4}{r}\right)+…+{ar}^{{n}−\mathrm{1}} \left({a}+\left({n}−\mathrm{2}\right){r}\right)+{ar}^{{n}} \left({a}+\left({n}−\mathrm{1}\right){r}\right) \\ $$$${rS}=\mathrm{0}+\left({a}^{\mathrm{2}} {r}\right)+\mathrm{0}+\left({a}^{\mathrm{2}} {r}^{\mathrm{2}} \right)+\mathrm{0}+\left({ar}^{\mathrm{3}} \right)+\mathrm{0}+\left({a}^{\mathrm{2}} {r}^{\mathrm{3}} \right)+\left(\mathrm{2}{ar}^{\mathrm{4}} \right)+{a}^{\mathrm{2}} {r}^{\mathrm{4}} +\mathrm{4}{ar}^{\mathrm{5}} +…+\left({a}^{\mathrm{2}} {r}^{{n}−\mathrm{1}} \right)+\left({n}−\mathrm{2}\right){ar}^{{n}} +{a}^{\mathrm{2}} {r}^{{n}} +{ar}^{{n}+\mathrm{1}} \left({n}−\mathrm{1}\right) \\ $$$$\:\:{S}={a}^{\mathrm{2}} +\left({a}^{\mathrm{2}} {r}\right)+{ar}^{\mathrm{2}} +\left({a}^{\mathrm{2}} {r}^{\mathrm{2}} \right)+\left(\mathrm{2}{ar}^{\mathrm{3}} \right)+\left({a}^{\mathrm{2}} {r}^{\mathrm{3}} \right)+\left(\mathrm{3}{ar}^{\mathrm{4}} \right)+…+\left({a}^{\mathrm{2}} {r}^{{n}−\mathrm{1}} \right)+\left({n}−\mathrm{1}\right){ar}^{{n}} \\ $$$$\Rightarrow\left({r}−\mathrm{1}\right){S}=−{a}^{\mathrm{2}} −{ar}^{\mathrm{2}} −{ar}^{\mathrm{3}} −{ar}^{\mathrm{4}} −…−{ar}^{{n}} −{ar}^{{n}+\mathrm{1}} +{a}^{\mathrm{2}} {r}^{{n}} +{nar}^{{n}+\mathrm{1}} \\ $$$$\left({r}−\mathrm{1}\right){S}={a}^{\mathrm{2}} {r}^{{n}} −{a}^{\mathrm{2}} −{ar}^{\mathrm{2}} \left(\mathrm{1}+{r}+{r}^{\mathrm{2}} +…+{r}^{{n}−\mathrm{2}} +{r}^{{n}−\mathrm{1}} \right)+{nar}^{{n}+\mathrm{1}} \\ $$$$\left({r}−\mathrm{1}\right){S}={a}^{\mathrm{2}} \left({r}^{{n}} −\mathrm{1}\right)+{nar}^{{n}+\mathrm{1}} −\frac{{ar}^{\mathrm{2}} \left({r}^{{n}} −\mathrm{1}\right)}{\left({r}−\mathrm{1}\right)} \\ $$$${S}=\frac{{r}^{{n}} −\mathrm{1}}{{r}−\mathrm{1}}\left({a}^{\mathrm{2}} −\frac{{ar}^{\mathrm{2}} }{{r}−\mathrm{1}}\right)+\frac{{nar}^{{n}+\mathrm{1}} }{{r}−\mathrm{1}} \\ $$$${S}=\frac{{nar}^{{n}+\mathrm{1}} }{{r}−\mathrm{1}}+\frac{{a}\left({r}^{{n}} −\mathrm{1}\right)\left({a}\left({r}−\mathrm{1}\right)−{r}^{\mathrm{2}} \right)}{\left({r}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${S}=\frac{{nar}^{{n}+\mathrm{1}} +{a}^{\mathrm{2}} \left({r}^{{n}} −\mathrm{1}\right)}{{r}−\mathrm{1}}−\frac{{ar}^{\mathrm{2}} \left({r}^{{n}} −\mathrm{1}\right)}{\left({r}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${If}\:{r}<\mathrm{1}\:{S}\:{can}\:{be}\:{divergent}\:{e}.{g}\:{let}\:{r}=−\mathrm{56}. \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 26/May/16
ThankS!
$$\mathcal{T}{hank}\mathcal{S}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *