Question Number 1156 by 112358 last updated on 06/Jul/15

$${Determine}\:{the}\:{general}\:{solution} \\ $$$${of}\:{the}\:{following}\:\:{linear}\:{diophantine} \\ $$$${equation}\:{for}\:\forall{N}\in\mathbb{Z}^{+} ,{m}\in\mathbb{Z}^{+} : \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{8}{N}=\mathrm{81}{m}+\mathrm{65}\:. \\ $$
Commented by prakash jain last updated on 06/Jul/15

$$\mathrm{N}\equiv\mathrm{1}×{m}+\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{8}\right) \\ $$$$\mathrm{m}\equiv\mathrm{7}\left(\mathrm{mod}\:\mathrm{8}\right) \\ $$
Answered by prakash jain last updated on 06/Jul/15
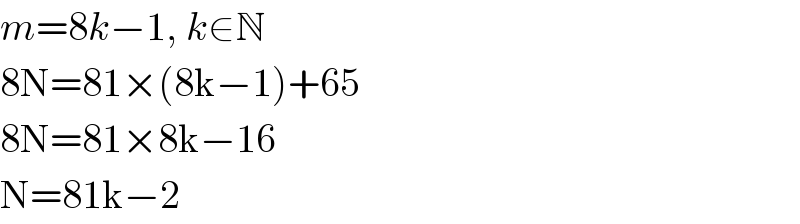
$${m}=\mathrm{8}{k}−\mathrm{1},\:{k}\in\mathbb{N} \\ $$$$\mathrm{8N}=\mathrm{81}×\left(\mathrm{8k}−\mathrm{1}\right)+\mathrm{65} \\ $$$$\mathrm{8N}=\mathrm{81}×\mathrm{8k}−\mathrm{16} \\ $$$$\mathrm{N}=\mathrm{81k}−\mathrm{2} \\ $$
