Question Number 72784 by Maclaurin Stickker last updated on 02/Nov/19

$${Determine}\:{the}\:{independent}\:{term}\:{of} \\ $$$${x}: \\ $$$$\left(\mathrm{3}{x}−\frac{\mathrm{2}}{{x}}\right)^{\mathrm{4}} \\ $$
Commented by mathmax by abdo last updated on 03/Nov/19
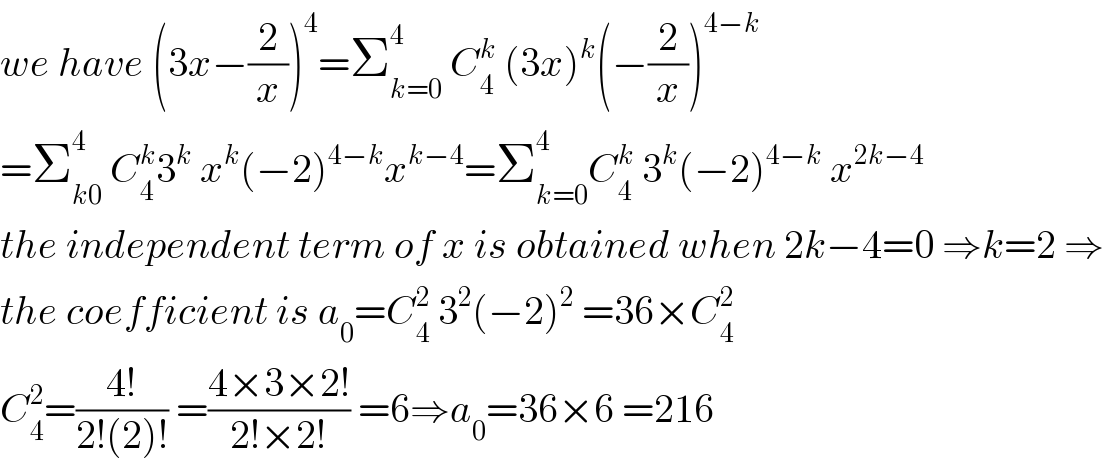
$${we}\:{have}\:\left(\mathrm{3}{x}−\frac{\mathrm{2}}{{x}}\right)^{\mathrm{4}} =\sum_{{k}=\mathrm{0}} ^{\mathrm{4}} \:{C}_{\mathrm{4}} ^{{k}} \:\left(\mathrm{3}{x}\right)^{{k}} \left(−\frac{\mathrm{2}}{{x}}\right)^{\mathrm{4}−{k}} \\ $$$$=\sum_{{k}\mathrm{0}} ^{\mathrm{4}} \:{C}_{\mathrm{4}} ^{{k}} \mathrm{3}^{{k}} \:{x}^{{k}} \left(−\mathrm{2}\right)^{\mathrm{4}−{k}} {x}^{{k}−\mathrm{4}} =\sum_{{k}=\mathrm{0}} ^{\mathrm{4}} {C}_{\mathrm{4}} ^{{k}} \:\mathrm{3}^{{k}} \left(−\mathrm{2}\right)^{\mathrm{4}−{k}} \:{x}^{\mathrm{2}{k}−\mathrm{4}} \\ $$$${the}\:{independent}\:{term}\:{of}\:{x}\:{is}\:{obtained}\:{when}\:\mathrm{2}{k}−\mathrm{4}=\mathrm{0}\:\Rightarrow{k}=\mathrm{2}\:\Rightarrow \\ $$$${the}\:{coefficient}\:{is}\:{a}_{\mathrm{0}} ={C}_{\mathrm{4}} ^{\mathrm{2}} \:\mathrm{3}^{\mathrm{2}} \left(−\mathrm{2}\right)^{\mathrm{2}} \:=\mathrm{36}×{C}_{\mathrm{4}} ^{\mathrm{2}} \\ $$$${C}_{\mathrm{4}} ^{\mathrm{2}} =\frac{\mathrm{4}!}{\mathrm{2}!\left(\mathrm{2}\right)!}\:=\frac{\mathrm{4}×\mathrm{3}×\mathrm{2}!}{\mathrm{2}!×\mathrm{2}!}\:=\mathrm{6}\Rightarrow{a}_{\mathrm{0}} =\mathrm{36}×\mathrm{6}\:=\mathrm{216} \\ $$
Answered by $@ty@m123 last updated on 02/Nov/19
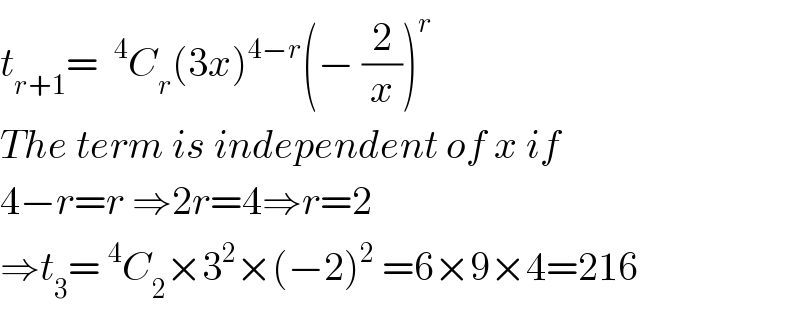
$${t}_{{r}+\mathrm{1}} =\:\:^{\mathrm{4}} {C}_{{r}} \left(\mathrm{3}{x}\right)^{\mathrm{4}−{r}} \left(−\:\frac{\mathrm{2}}{{x}}\right)^{{r}} \\ $$$${The}\:{term}\:{is}\:{independent}\:{of}\:{x}\:{if} \\ $$$$\mathrm{4}−{r}={r}\:\Rightarrow\mathrm{2}{r}=\mathrm{4}\Rightarrow{r}=\mathrm{2} \\ $$$$\Rightarrow{t}_{\mathrm{3}} =\:^{\mathrm{4}} {C}_{\mathrm{2}} ×\mathrm{3}^{\mathrm{2}} ×\left(−\mathrm{2}\right)^{\mathrm{2}} \:=\mathrm{6}×\mathrm{9}×\mathrm{4}=\mathrm{216} \\ $$
