Question Number 751 by 112358 last updated on 06/Mar/15

$${Determine}\:{the}\:{number}\:{of}\:{integral} \\ $$$${factors}\:{of}\:\mathrm{105840},\:{excluding}\:\mathrm{1}\: \\ $$$${and}\:\mathrm{105840}. \\ $$$$ \\ $$$$ \\ $$
Answered by prakash jain last updated on 06/Mar/15
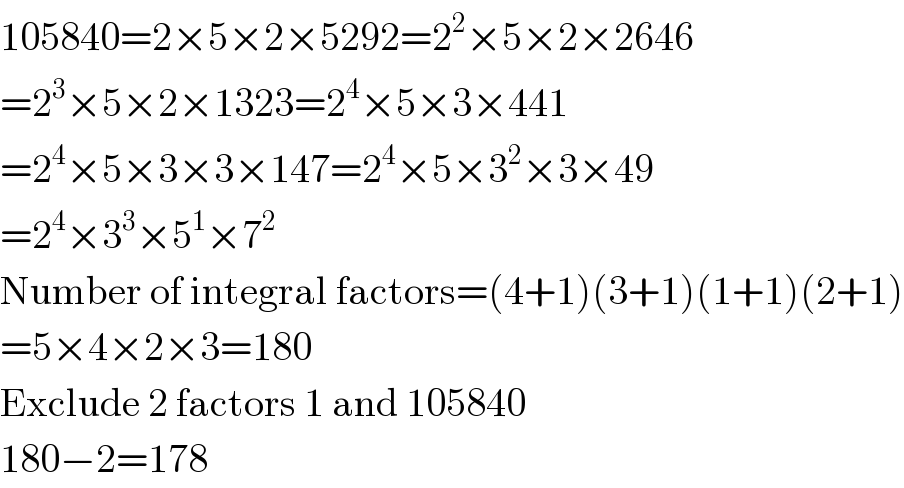
$$\mathrm{105840}=\mathrm{2}×\mathrm{5}×\mathrm{2}×\mathrm{5292}=\mathrm{2}^{\mathrm{2}} ×\mathrm{5}×\mathrm{2}×\mathrm{2646} \\ $$$$=\mathrm{2}^{\mathrm{3}} ×\mathrm{5}×\mathrm{2}×\mathrm{1323}=\mathrm{2}^{\mathrm{4}} ×\mathrm{5}×\mathrm{3}×\mathrm{441} \\ $$$$=\mathrm{2}^{\mathrm{4}} ×\mathrm{5}×\mathrm{3}×\mathrm{3}×\mathrm{147}=\mathrm{2}^{\mathrm{4}} ×\mathrm{5}×\mathrm{3}^{\mathrm{2}} ×\mathrm{3}×\mathrm{49} \\ $$$$=\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{3}} ×\mathrm{5}^{\mathrm{1}} ×\mathrm{7}^{\mathrm{2}} \\ $$$$\mathrm{Number}\:\mathrm{of}\:\mathrm{integral}\:\mathrm{factors}=\left(\mathrm{4}+\mathrm{1}\right)\left(\mathrm{3}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{2}+\mathrm{1}\right) \\ $$$$=\mathrm{5}×\mathrm{4}×\mathrm{2}×\mathrm{3}=\mathrm{180} \\ $$$$\mathrm{Exclude}\:\mathrm{2}\:\mathrm{factors}\:\mathrm{1}\:\mathrm{and}\:\mathrm{105840} \\ $$$$\mathrm{180}−\mathrm{2}=\mathrm{178} \\ $$
