Question Number 907 by Yugi last updated on 19/Apr/15
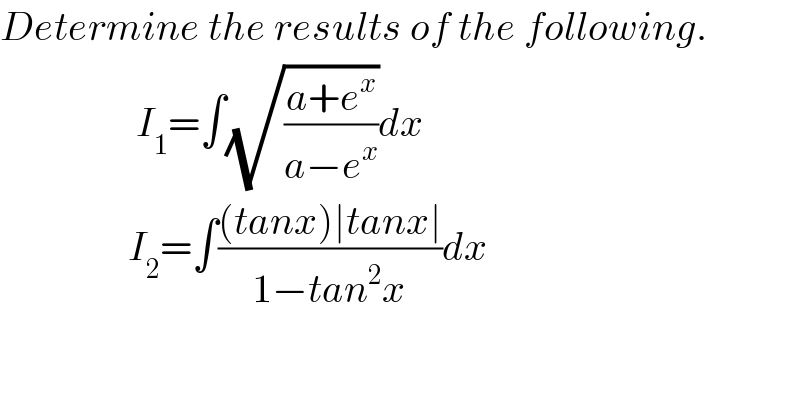
$${Determine}\:{the}\:{results}\:{of}\:{the}\:{following}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{I}_{\mathrm{1}} =\int\sqrt{\frac{{a}+{e}^{{x}} }{{a}−{e}^{{x}} }}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{I}_{\mathrm{2}} =\int\frac{\left({tanx}\right)\mid{tanx}\mid}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}{dx} \\ $$
Commented by prakash jain last updated on 21/Apr/15
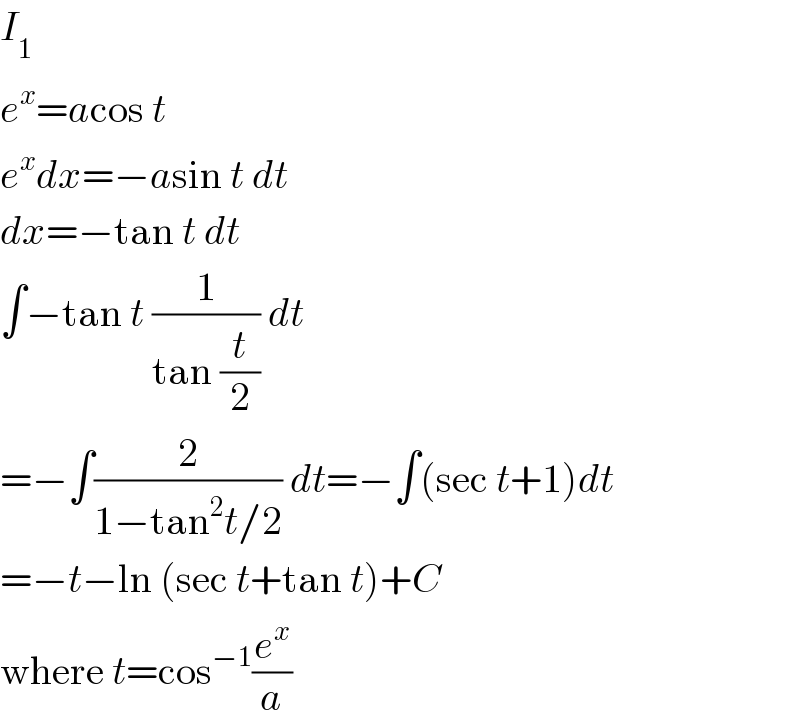
$${I}_{\mathrm{1}} \\ $$$${e}^{{x}} ={a}\mathrm{cos}\:{t} \\ $$$${e}^{{x}} {dx}=−{a}\mathrm{sin}\:{t}\:{dt} \\ $$$${dx}=−\mathrm{tan}\:{t}\:{dt} \\ $$$$\int−\mathrm{tan}\:{t}\:\frac{\mathrm{1}}{\mathrm{tan}\:\frac{{t}}{\mathrm{2}}}\:{dt} \\ $$$$=−\int\frac{\mathrm{2}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} {t}/\mathrm{2}}\:{dt}=−\int\left(\mathrm{sec}\:{t}+\mathrm{1}\right){dt} \\ $$$$=−{t}−\mathrm{ln}\:\left(\mathrm{sec}\:{t}+\mathrm{tan}\:{t}\right)+{C} \\ $$$$\mathrm{where}\:{t}=\mathrm{cos}^{−\mathrm{1}} \frac{{e}^{{x}} }{{a}} \\ $$
