Menu Close

Determine-the-smallest-value-of-the-form-f-u-v-5v-2-5u-2-1-2u-v-where-u-v-R-

Tinku Tara 0 Comments
Pin




Question Number 514 by 112358 last updated on 25/Jan/15
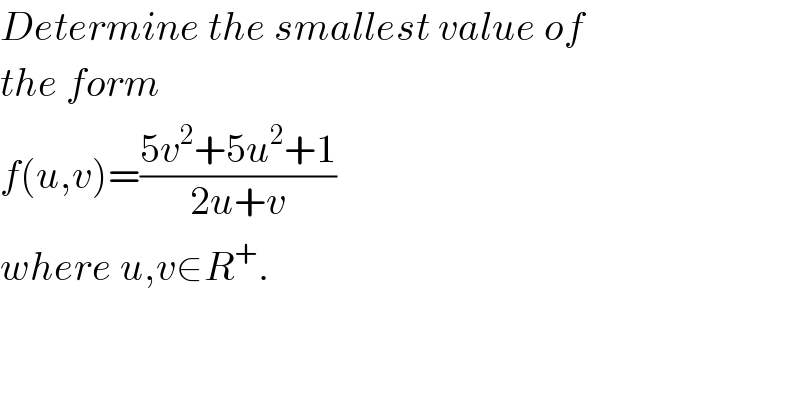
Determine the smallest value of the form f(u,v)=((5v^2 +5u^2 +1)/(2u+v)) where u,v∈R^+ .
$${Determine}\:{the}\:{smallest}\:{value}\:{of} \\ $$$${the}\:{form} \\ $$$${f}\left({u},{v}\right)=\frac{\mathrm{5}{v}^{\mathrm{2}} +\mathrm{5}{u}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{u}+{v}} \\ $$$${where}\:{u},{v}\in{R}^{+} . \\ $$
Answered by prakash jain last updated on 23/Jan/15
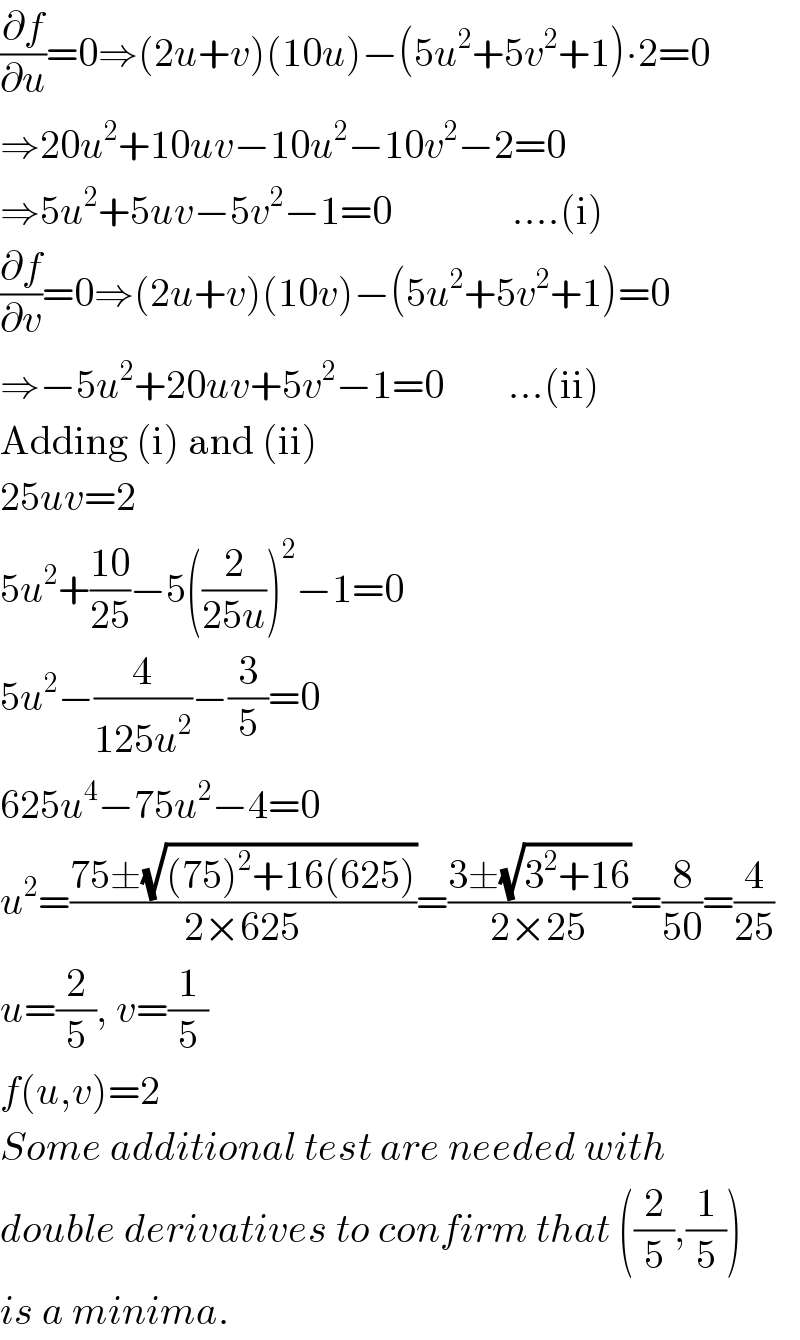
(∂f/∂u)=0⇒(2u+v)(10u)−(5u^2 +5v^2 +1)∙2=0 ⇒20u^2 +10uv−10u^2 −10v^2 −2=0 ⇒5u^2 +5uv−5v^2 −1=0 ....(i) (∂f/∂v)=0⇒(2u+v)(10v)−(5u^2 +5v^2 +1)=0 ⇒−5u^2 +20uv+5v^2 −1=0 ...(ii) Adding (i) and (ii) 25uv=2 5u^2 +((10)/(25))−5((2/(25u)))^2 −1=0 5u^2 −(4/(125u^2 ))−(3/5)=0 625u^4 −75u^2 −4=0 u^2 =((75±(√((75)^2 +16(625))))/(2×625))=((3±(√(3^2 +16)))/(2×25))=(8/(50))=(4/(25)) u=(2/5), v=(1/5) f(u,v)=2 Some additional test are needed with double derivatives to confirm that ((2/5),(1/5)) is a minima.
$$\frac{\partial{f}}{\partial{u}}=\mathrm{0}\Rightarrow\left(\mathrm{2}{u}+{v}\right)\left(\mathrm{10}{u}\right)−\left(\mathrm{5}{u}^{\mathrm{2}} +\mathrm{5}{v}^{\mathrm{2}} +\mathrm{1}\right)\centerdot\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{20}{u}^{\mathrm{2}} +\mathrm{10}{uv}−\mathrm{10}{u}^{\mathrm{2}} −\mathrm{10}{v}^{\mathrm{2}} −\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{5}{u}^{\mathrm{2}} +\mathrm{5}{uv}−\mathrm{5}{v}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left(\mathrm{i}\right) \\ $$$$\frac{\partial{f}}{\partial{v}}=\mathrm{0}\Rightarrow\left(\mathrm{2}{u}+{v}\right)\left(\mathrm{10}{v}\right)−\left(\mathrm{5}{u}^{\mathrm{2}} +\mathrm{5}{v}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow−\mathrm{5}{u}^{\mathrm{2}} +\mathrm{20}{uv}+\mathrm{5}{v}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\:\:\:\:\:\:\:…\left(\mathrm{ii}\right) \\ $$$$\mathrm{Adding}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{25}{uv}=\mathrm{2} \\ $$$$\mathrm{5}{u}^{\mathrm{2}} +\frac{\mathrm{10}}{\mathrm{25}}−\mathrm{5}\left(\frac{\mathrm{2}}{\mathrm{25}{u}}\right)^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{5}{u}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{125}{u}^{\mathrm{2}} }−\frac{\mathrm{3}}{\mathrm{5}}=\mathrm{0} \\ $$$$\mathrm{625}{u}^{\mathrm{4}} −\mathrm{75}{u}^{\mathrm{2}} −\mathrm{4}=\mathrm{0} \\ $$$${u}^{\mathrm{2}} =\frac{\mathrm{75}\pm\sqrt{\left(\mathrm{75}\right)^{\mathrm{2}} +\mathrm{16}\left(\mathrm{625}\right)}}{\mathrm{2}×\mathrm{625}}=\frac{\mathrm{3}\pm\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{16}}}{\mathrm{2}×\mathrm{25}}=\frac{\mathrm{8}}{\mathrm{50}}=\frac{\mathrm{4}}{\mathrm{25}} \\ $$$${u}=\frac{\mathrm{2}}{\mathrm{5}},\:{v}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${f}\left({u},{v}\right)=\mathrm{2} \\ $$$${Some}\:{additional}\:{test}\:{are}\:{needed}\:{with} \\ $$$${double}\:{derivatives}\:{to}\:{confirm}\:{that}\:\left(\frac{\mathrm{2}}{\mathrm{5}},\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$${is}\:{a}\:{minima}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *