Question Number 131097 by dw last updated on 01/Feb/21
![Determine the value of (S/π), if S is the sum, in radians, all equation solutions contained in the interval [0,14π]. the equation is: cos(x)+cos^5 (x)+cos(7x)=3](https://www.tinkutara.com/question/Q131097.png)
Answered by MJS_new last updated on 01/Feb/21
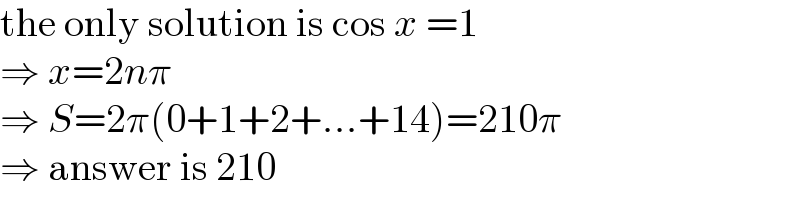
Commented by dw last updated on 01/Feb/21
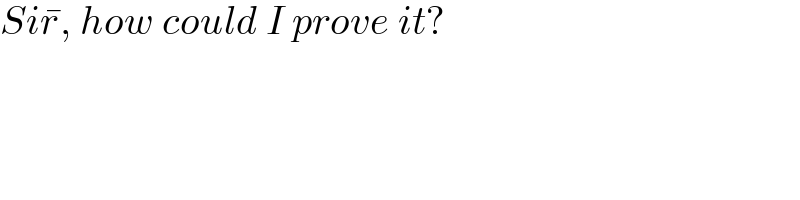
Commented by dw last updated on 01/Feb/21

Answered by MJS_new last updated on 01/Feb/21
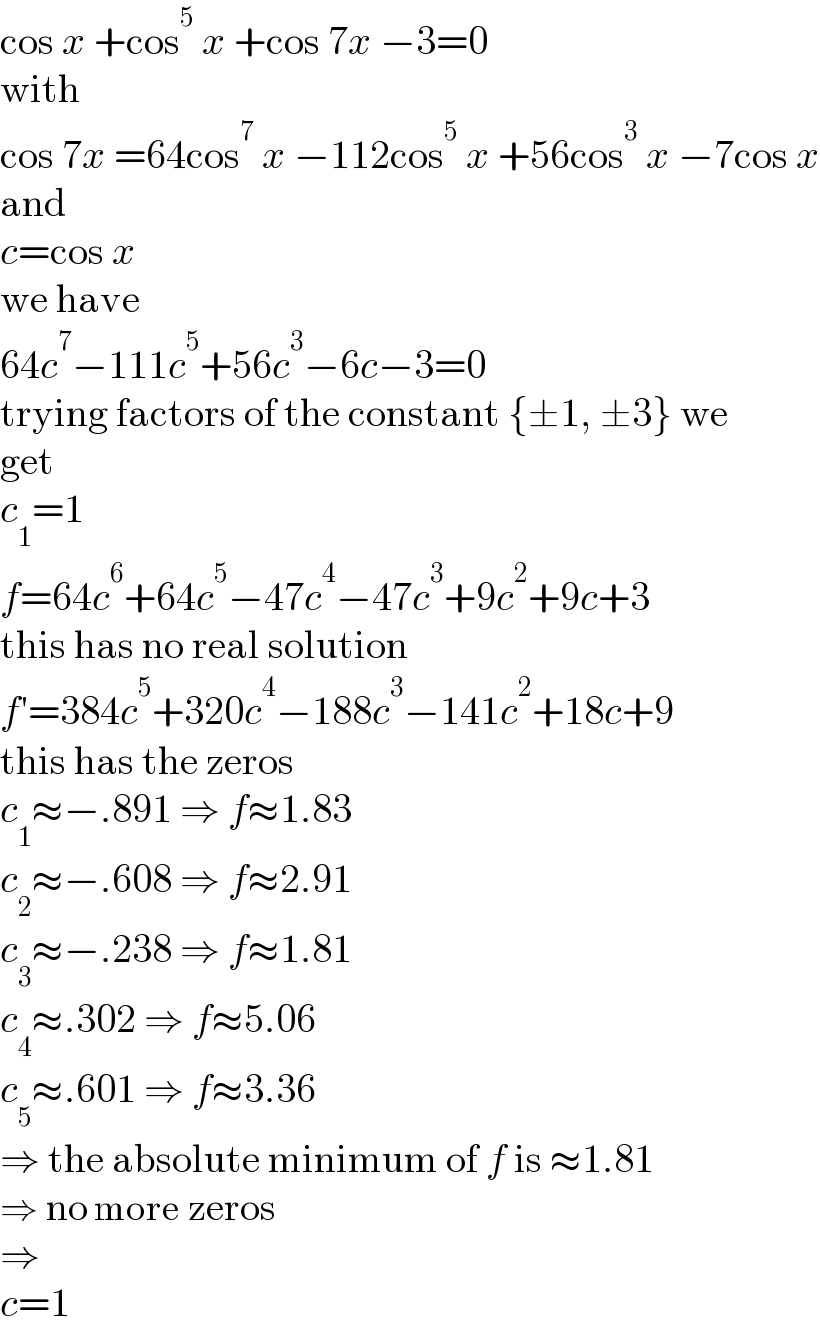
Commented by dw last updated on 01/Feb/21

