Question Number 142228 by mathmax by abdo last updated on 28/May/21

$$\mathrm{developpf}\left(\mathrm{x}\right)=\frac{\mathrm{2}}{\mathrm{3}+\mathrm{cosx}}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$
Answered by mathmax by abdo last updated on 28/May/21
![another way f is even ⇒f(x)=(a_o /2) +Σ_(n=1) ^∞ a_n cos(nx) a_n =(2/T)∫_([T]) f(x)cos(nx) =(2/(2π))∫_0 ^(2π) (2/(3+cosx))cos(nx)dx =(2/π)∫_0 ^(2π) ((cos(nx))/(3+cosx))dx ⇒(π/2)a_n =∫_0 ^(2π) ((cos(nx))/(3+cosx))dx =_(e^(ix) =z) ∫_(∣z∣=1) (((z^n +z^(−n) )/2)/(3+((z+z^(−1) )/2)))(dz/(iz))=−2i∫_(∣z∣=1) ((z^n +z^(−n) )/((6+z+z^(−1) )z))dz =−2i∫_(∣z∣=1) ((z^n +z^(−n) )/(z^2 +6z +1))dz let ϕ(z)=((z^n +z^(−n) )/(z^2 +6z +1)) poles of ϕ! Δ^′ =8 ⇒z_1 =−3+2(√2) and z_2 =−3−2(√2) ⇒ϕ(z)=((z^n +z^(−n) )/((z−z_1 )(z−z_2 ))) ∣z_1 ∣−1 =3−2(√2)−1 =2−2(√2)<0 ⇒∣z_1 ∣<1 ∣z_2 ∣−1=3+2(√2)−1 =2+2(√2)>0 (out of circle) ⇒ ∫_(∣z∣=1) ϕ(z)dz =2iπ Res(ϕ,z_1 ) =2iπ((z_1 ^n +z_1 ^(−n) )/(z_1 −z_2 )) =((2iπ)/(4(√2))){ (−3+2(√2))^n +(−3+2(√2))^(−n) } =((iπ)/(2(√2))){ (−3+2(√2))^n +(−3+2(√2))^(−n) } ⇒ (π/2)a_n =−2i×((iπ)/(2(√2))){(−3+2(√2))^n +(−3+2(√2))^(−n) } =(π/( (√2))){(−3+2(√2))^n [+(−3+2(√2))^n } ⇒a_n =(√2)(−1)^n { (3−2(√2))^n +(3−2(√2))^(−n) } a_o =2(√2)=(2/π)∫_0 ^(2π) (dx/(3+cosx)) ⇒ (2/(3+cosx))=(√2)+(√2)Σ_(n=1) ^∞ (−1)^n {(3−2(√2))^n +(3−2(√2))^(−n) }cos(nx)](https://www.tinkutara.com/question/Q142242.png)
$$\mathrm{another}\:\mathrm{way}\:\mathrm{f}\:\mathrm{is}\:\mathrm{even}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{a}_{\mathrm{o}} }{\mathrm{2}}\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{a}_{\mathrm{n}} \mathrm{cos}\left(\mathrm{nx}\right) \\ $$$$\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{2}}{\mathrm{T}}\int_{\left[\mathrm{T}\right]} \:\mathrm{f}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{nx}\right)\:=\frac{\mathrm{2}}{\mathrm{2}\pi}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{2}}{\mathrm{3}+\mathrm{cosx}}\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{2}}{\pi}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{cos}\left(\mathrm{nx}\right)}{\mathrm{3}+\mathrm{cosx}}\mathrm{dx}\:\Rightarrow\frac{\pi}{\mathrm{2}}\mathrm{a}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{cos}\left(\mathrm{nx}\right)}{\mathrm{3}+\mathrm{cosx}}\mathrm{dx} \\ $$$$=_{\mathrm{e}^{\mathrm{ix}} =\mathrm{z}} \:\:\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{\frac{\mathrm{z}^{\mathrm{n}} +\mathrm{z}^{−\mathrm{n}} }{\mathrm{2}}}{\mathrm{3}+\frac{\mathrm{z}+\mathrm{z}^{−\mathrm{1}} }{\mathrm{2}}}\frac{\mathrm{dz}}{\mathrm{iz}}=−\mathrm{2i}\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{z}^{\mathrm{n}} +\mathrm{z}^{−\mathrm{n}} }{\left(\mathrm{6}+\mathrm{z}+\mathrm{z}^{−\mathrm{1}} \right)\mathrm{z}}\mathrm{dz} \\ $$$$=−\mathrm{2i}\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{z}^{\mathrm{n}} +\mathrm{z}^{−\mathrm{n}} }{\mathrm{z}^{\mathrm{2}} +\mathrm{6z}\:+\mathrm{1}}\mathrm{dz}\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{n}} +\mathrm{z}^{−\mathrm{n}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{6z}\:+\mathrm{1}}\:\:\mathrm{poles}\:\mathrm{of}\:\varphi! \\ $$$$\Delta^{'} \:=\mathrm{8}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =−\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{n}} +\mathrm{z}^{−\mathrm{n}} }{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)} \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid−\mathrm{1}\:=\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\:=\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}<\mathrm{0}\:\:\Rightarrow\mid\mathrm{z}_{\mathrm{1}} \mid<\mathrm{1} \\ $$$$\mid\mathrm{z}_{\mathrm{2}} \mid−\mathrm{1}=\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\:=\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}>\mathrm{0}\:\:\left(\mathrm{out}\:\mathrm{of}\:\mathrm{circle}\right)\:\Rightarrow \\ $$$$\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right)\:=\mathrm{2i}\pi\frac{\mathrm{z}_{\mathrm{1}} ^{\mathrm{n}} \:+\mathrm{z}_{\mathrm{1}} ^{−\mathrm{n}} }{\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2i}\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\left\{\:\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} \:+\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{−\mathrm{n}} \right\} \\ $$$$=\frac{\mathrm{i}\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} \:+\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{−\mathrm{n}} \right\}\:\Rightarrow \\ $$$$\frac{\pi}{\mathrm{2}}\mathrm{a}_{\mathrm{n}} =−\mathrm{2i}×\frac{\mathrm{i}\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} \:+\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{−\mathrm{n}} \right\} \\ $$$$=\frac{\pi}{\:\sqrt{\mathrm{2}}}\left\{\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} \left[+\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} \right\}\right. \\ $$$$\Rightarrow\mathrm{a}_{\mathrm{n}} =\sqrt{\mathrm{2}}\left(−\mathrm{1}\right)^{\mathrm{n}} \left\{\:\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} \:+\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)^{−\mathrm{n}} \right\} \\ $$$$\mathrm{a}_{\mathrm{o}} =\mathrm{2}\sqrt{\mathrm{2}}=\frac{\mathrm{2}}{\pi}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{dx}}{\mathrm{3}+\mathrm{cosx}}\:\Rightarrow \\ $$$$\frac{\mathrm{2}}{\mathrm{3}+\mathrm{cosx}}=\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \left\{\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} \:+\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)^{−\mathrm{n}} \right\}\mathrm{cos}\left(\mathrm{nx}\right) \\ $$
Commented by Mathspace last updated on 28/May/21
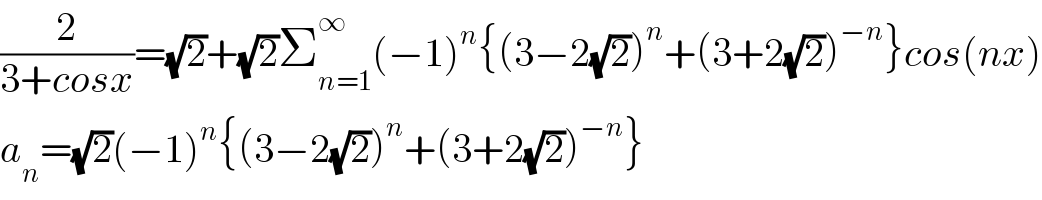
$$\frac{\mathrm{2}}{\mathrm{3}+{cosx}}=\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \left\{\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)^{{n}} +\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{−{n}} \right\}{cos}\left({nx}\right) \\ $$$${a}_{{n}} =\sqrt{\mathrm{2}}\left(−\mathrm{1}\right)^{{n}} \left\{\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)^{{n}} +\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{−{n}} \right\} \\ $$
