Menu Close

deveopp-g-x-1-sin-nx-at-fourier-series-x-kpi-n-

Tinku Tara 0 Comments
Pin




Question Number 142229 by mathmax by abdo last updated on 28/May/21
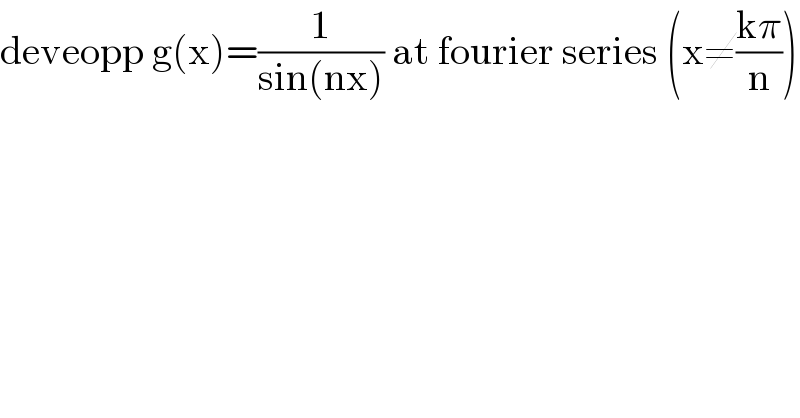
deveopp g(x)=(1/(sin(nx))) at fourier series (x≠((kπ)/n))
$$\mathrm{deveopp}\:\mathrm{g}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{sin}\left(\mathrm{nx}\right)}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{series}\:\left(\mathrm{x}\neq\frac{\mathrm{k}\pi}{\mathrm{n}}\right) \\ $$
Answered by mathmax by abdo last updated on 29/May/21
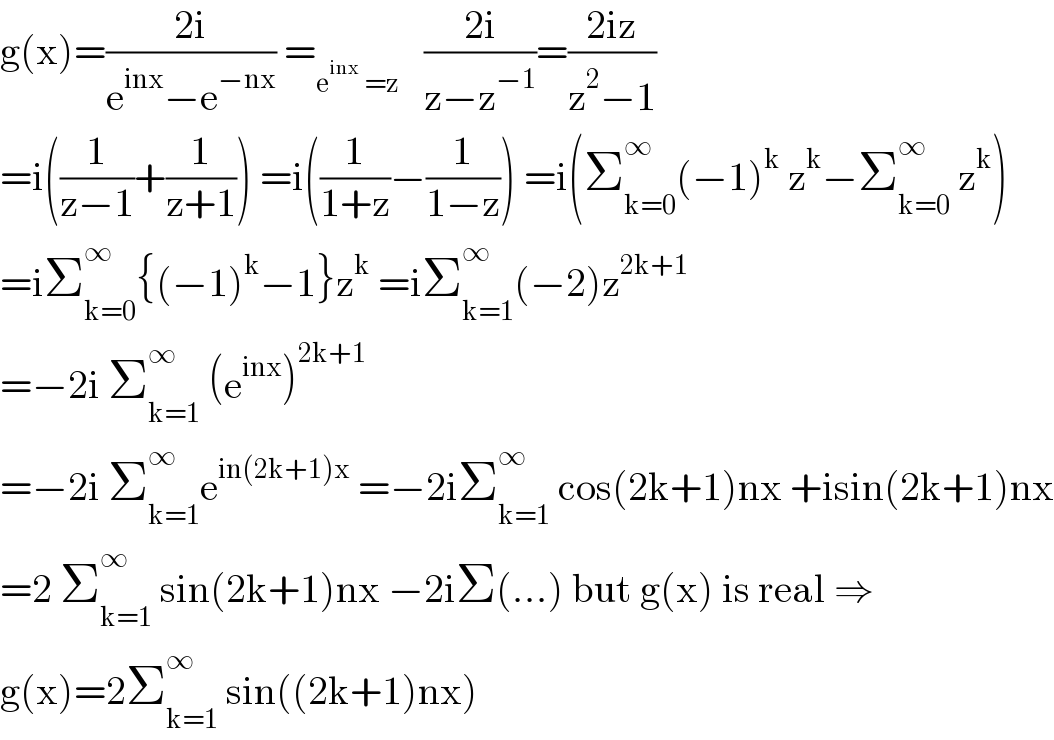
g(x)=((2i)/(e^(inx) −e^(−nx) )) =_(e^(inx) =z) ((2i)/(z−z^(−1) ))=((2iz)/(z^2 −1)) =i((1/(z−1))+(1/(z+1))) =i((1/(1+z))−(1/(1−z))) =i(Σ_(k=0) ^∞ (−1)^k z^k −Σ_(k=0) ^∞ z^k ) =iΣ_(k=0) ^∞ {(−1)^k −1}z^k =iΣ_(k=1) ^∞ (−2)z^(2k+1) =−2i Σ_(k=1) ^∞ (e^(inx) )^(2k+1) =−2i Σ_(k=1) ^∞ e^(in(2k+1)x) =−2iΣ_(k=1) ^∞ cos(2k+1)nx +isin(2k+1)nx =2 Σ_(k=1) ^∞ sin(2k+1)nx −2iΣ(...) but g(x) is real ⇒ g(x)=2Σ_(k=1) ^∞ sin((2k+1)nx)
$$\mathrm{g}\left(\mathrm{x}\right)=\frac{\mathrm{2i}}{\mathrm{e}^{\mathrm{inx}} −\mathrm{e}^{−\mathrm{nx}} }\:=_{\mathrm{e}^{\mathrm{inx}} \:=\mathrm{z}} \:\:\:\frac{\mathrm{2i}}{\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }=\frac{\mathrm{2iz}}{\mathrm{z}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\mathrm{i}\left(\frac{\mathrm{1}}{\mathrm{z}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{z}+\mathrm{1}}\right)\:=\mathrm{i}\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{z}}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{z}}\right)\:=\mathrm{i}\left(\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{z}^{\mathrm{k}} −\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\mathrm{z}^{\mathrm{k}} \right) \\ $$$$=\mathrm{i}\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \left\{\left(−\mathrm{1}\right)^{\mathrm{k}} −\mathrm{1}\right\}\mathrm{z}^{\mathrm{k}} \:=\mathrm{i}\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \left(−\mathrm{2}\right)\mathrm{z}^{\mathrm{2k}+\mathrm{1}} \\ $$$$=−\mathrm{2i}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\left(\mathrm{e}^{\mathrm{inx}} \right)^{\mathrm{2k}+\mathrm{1}} \\ $$$$=−\mathrm{2i}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \mathrm{e}^{\mathrm{in}\left(\mathrm{2k}+\mathrm{1}\right)\mathrm{x}} \:=−\mathrm{2i}\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\mathrm{cos}\left(\mathrm{2k}+\mathrm{1}\right)\mathrm{nx}\:+\mathrm{isin}\left(\mathrm{2k}+\mathrm{1}\right)\mathrm{nx} \\ $$$$=\mathrm{2}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\mathrm{sin}\left(\mathrm{2k}+\mathrm{1}\right)\mathrm{nx}\:−\mathrm{2i}\Sigma\left(…\right)\:\mathrm{but}\:\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{real}\:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{2}\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\mathrm{sin}\left(\left(\mathrm{2k}+\mathrm{1}\right)\mathrm{nx}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *