Question Number 6180 by FilupSmith last updated on 17/Jun/16
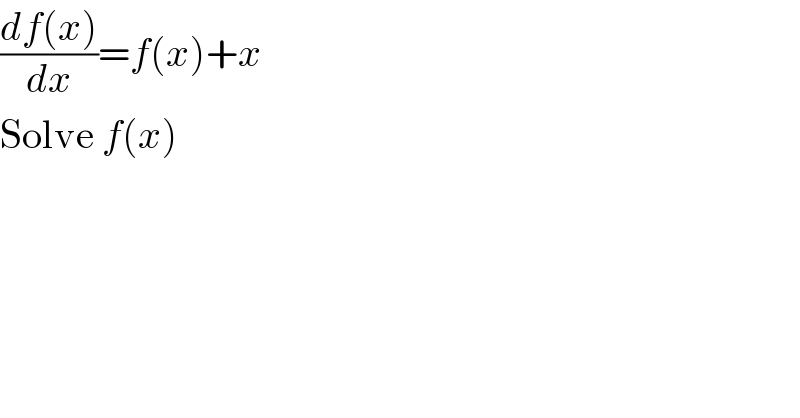
$$\frac{{df}\left({x}\right)}{{dx}}={f}\left({x}\right)+{x} \\ $$$$\mathrm{Solve}\:{f}\left({x}\right) \\ $$
Commented by 123456 last updated on 17/Jun/16
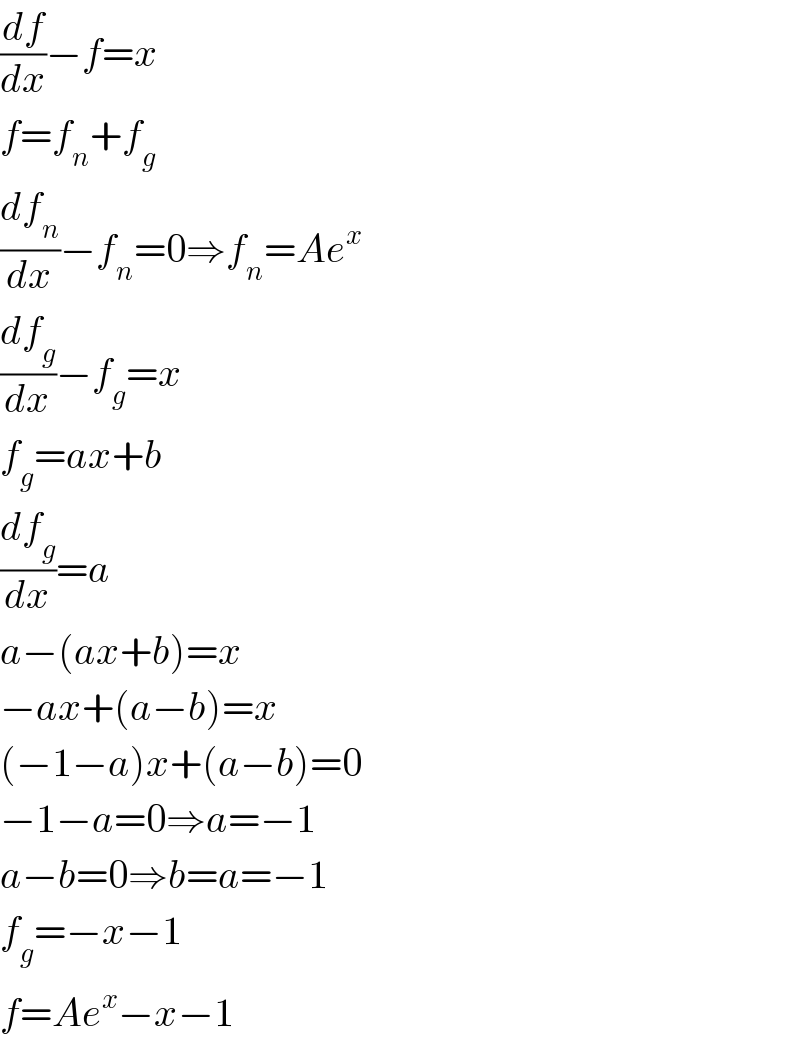
$$\frac{{df}}{{dx}}−{f}={x} \\ $$$${f}={f}_{{n}} +{f}_{{g}} \\ $$$$\frac{{df}_{{n}} }{{dx}}−{f}_{{n}} =\mathrm{0}\Rightarrow{f}_{{n}} ={Ae}^{{x}} \\ $$$$\frac{{df}_{{g}} }{{dx}}−{f}_{{g}} ={x} \\ $$$${f}_{{g}} ={ax}+{b} \\ $$$$\frac{{df}_{{g}} }{{dx}}={a} \\ $$$${a}−\left({ax}+{b}\right)={x} \\ $$$$−{ax}+\left({a}−{b}\right)={x} \\ $$$$\left(−\mathrm{1}−{a}\right){x}+\left({a}−{b}\right)=\mathrm{0} \\ $$$$−\mathrm{1}−{a}=\mathrm{0}\Rightarrow{a}=−\mathrm{1} \\ $$$${a}−{b}=\mathrm{0}\Rightarrow{b}={a}=−\mathrm{1} \\ $$$${f}_{{g}} =−{x}−\mathrm{1} \\ $$$${f}={Ae}^{{x}} −{x}−\mathrm{1} \\ $$
Commented by Rasheed Soomro last updated on 19/Jun/16
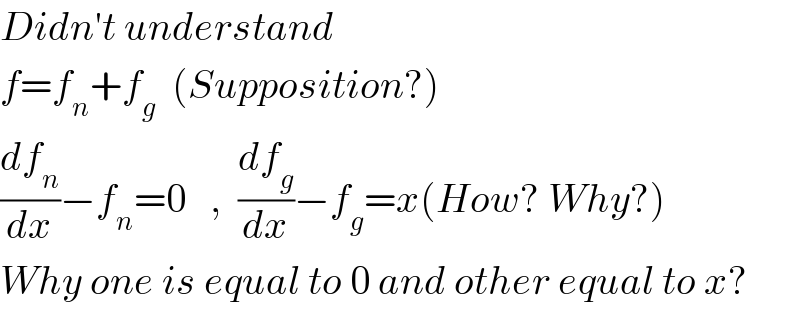
$${Didn}'{t}\:{understand} \\ $$$${f}={f}_{{n}} +{f}_{{g}} \:\:\left({Supposition}?\right) \\ $$$$\frac{{df}_{{n}} }{{dx}}−{f}_{{n}} =\mathrm{0}\:\:\:,\:\:\frac{{df}_{{g}} }{{dx}}−{f}_{{g}} ={x}\left({How}?\:{Why}?\right) \\ $$$${Why}\:{one}\:{is}\:{equal}\:{to}\:\mathrm{0}\:{and}\:{other}\:{equal}\:{to}\:{x}? \\ $$
Commented by prakash jain last updated on 20/Jun/16

$${y}'−{y}={x} \\ $$$$\mathrm{Let}\:\mathrm{us}\:\mathrm{say}\:{y}={f}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{such}\:\mathrm{that} \\ $$$${f}_{\mathrm{1}} '−{f}_{\mathrm{1}} ={x} \\ $$$$\mathrm{Also}\:\mathrm{assume}\:{f}_{\mathrm{2}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{such}\:\mathrm{that} \\ $$$${f}_{\mathrm{2}} '−{f}_{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{Now}\:\mathrm{for}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{of}\:{y} \\ $$$${y}={f}_{\mathrm{1}} +{kf}_{\mathrm{2}} \\ $$$${y}'={f}_{\mathrm{1}} '+{kf}_{\mathrm{2}} ' \\ $$$${y}'−{y}={f}_{\mathrm{1}} '+{kf}_{\mathrm{2}} '−{f}_{\mathrm{1}} −{f}_{\mathrm{2}} \\ $$$$={f}_{\mathrm{1}} '−{f}_{\mathrm{1}} +{k}\left({f}_{\mathrm{2}} '−{f}_{\mathrm{2}} \right)={x}+{k}\centerdot\mathrm{0}={x} \\ $$$$\mathrm{So}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{has}\:\mathrm{2}\:\mathrm{parts} \\ $$$$\mathrm{homogenous}\:\mathrm{solution}\:\left({f}_{\mathrm{2}} \right) \\ $$$$\mathrm{particular}\:\mathrm{solution}\:\left({f}_{\mathrm{1}} \right) \\ $$$${any}\:{multiple}\:{of}\:{homegenous}\:{solution}\:{can} \\ $$$${be}\:{added}\:{to}\:{particular}\:{solution}\:{and}\:{the}\:{sum} \\ $$$${will}\:{still}\:{satisfy}\:{differential}\:{equation}. \\ $$
Commented by Rasheed Soomro last updated on 21/Jun/16

$$\mathbb{TH}\mathcal{AN}\mathbb{X}! \\ $$
