Menu Close

differentiate-each-function-from-first-principle-1-f-x-1-1-x-2-f-x-1-2x-3-3-f-x-sin2x-4-f-x-co2x-

Tinku Tara 0 Comments
Pin




Question Number 11920 by carrot last updated on 05/Apr/17
differentiate each function from first principle 1)f (x) = 1+(1/x) 2)f(x) = (1/(2x+3)) 3) f(x)=sin2x 4)f(x)=co2x
$${differentiate}\:{each}\:{function}\:{from}\:{first}\:{principle} \\ $$$$\left.\mathrm{1}\right){f}\:\left({x}\right)\:=\:\mathrm{1}+\frac{\mathrm{1}}{{x}} \\ $$$$\left.\mathrm{2}\right){f}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{3}}\: \\ $$$$\left.\mathrm{3}\right)\:{f}\left({x}\right)={sin}\mathrm{2}{x} \\ $$$$\left.\mathrm{4}\right){f}\left({x}\right)={co}\mathrm{2}{x} \\ $$$$ \\ $$
Answered by sandy_suhendra last updated on 05/Apr/17
1)f(x)=1+x^(−1) f ′(x)=−x^(−2) =((−1)/x^2 ) 2)f(x)=(2x+3)^(−1) f ′(x)=−1(2x+3)^(−2) (2)=((−2)/((2x+3)^2 )) 3)f ′(x)=2cos2x 4)f ′(x)=−2sin2x
$$\left.\mathrm{1}\right)\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}+\mathrm{x}^{−\mathrm{1}} \\ $$$$\:\:\:\:\:\mathrm{f}\:'\left(\mathrm{x}\right)=−\mathrm{x}^{−\mathrm{2}} =\frac{−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{2x}+\mathrm{3}\right)^{−\mathrm{1}} \\ $$$$\:\:\:\:\mathrm{f}\:'\left(\mathrm{x}\right)=−\mathrm{1}\left(\mathrm{2x}+\mathrm{3}\right)^{−\mathrm{2}} \left(\mathrm{2}\right)=\frac{−\mathrm{2}}{\left(\mathrm{2x}+\mathrm{3}\right)^{\mathrm{2}} }\:\:\:\:\:\: \\ $$$$\left.\mathrm{3}\right)\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{2cos2x} \\ $$$$\left.\mathrm{4}\right)\mathrm{f}\:'\left(\mathrm{x}\right)=−\mathrm{2sin2x} \\ $$
Commented by carrot last updated on 05/Apr/17
oh what you did was differentiate it and thats not what they asked for
$${oh}\:{what}\:{you}\:{did}\:{was}\:{differentiate}\:{it}\:{and}\:{thats}\:{not}\:{what}\:{they}\:{asked}\:{for} \\ $$
Commented by sandy_suhendra last updated on 06/Apr/17
oh sorry because I don′t understand with the question but I have fixed for no 3 and 4
$$\mathrm{oh}\:\mathrm{sorry}\:\mathrm{because}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{with}\:\mathrm{the}\:\mathrm{question}\:\:\:\:\: \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{have}\:\mathrm{fixed}\:\mathrm{for}\:\mathrm{no}\:\mathrm{3}\:\mathrm{and}\:\mathrm{4} \\ $$
Answered by FilupS last updated on 05/Apr/17
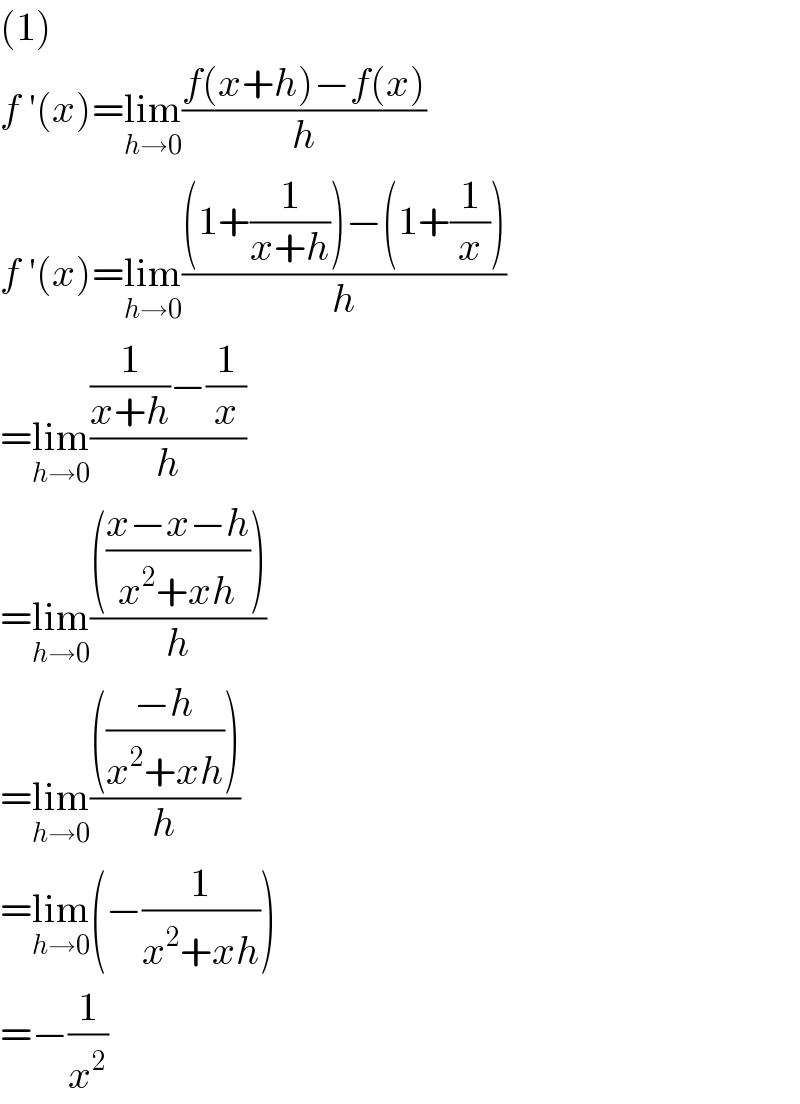
(1) f ′(x)=lim_(h→0) ((f(x+h)−f(x))/h) f ′(x)=lim_(h→0) (((1+(1/(x+h)))−(1+(1/x)))/h) =lim_(h→0) (((1/(x+h))−(1/x))/h) =lim_(h→0) (((((x−x−h)/(x^2 +xh))))/h) =lim_(h→0) (((((−h)/(x^2 +xh))))/h) =lim_(h→0) (−(1/(x^2 +xh))) =−(1/x^2 )
$$\left(\mathrm{1}\right) \\ $$$${f}\:'\left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}} \\ $$$${f}\:'\left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}+{h}}\right)−\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{{x}+{h}}−\frac{\mathrm{1}}{{x}}}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{{x}−{x}−{h}}{{x}^{\mathrm{2}} +{xh}}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{−{h}}{{x}^{\mathrm{2}} +{xh}}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{xh}}\right) \\ $$$$=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$
Answered by FilupS last updated on 05/Apr/17
(2) f ′(x)=lim_(h→0) ((f(x+h)−f(x))/h) f ′(x)=lim_(h→0) ((((1/(2x+2h+3)))−((1/(2x+3))))/h) =lim_(h→0) ((((1/(2x+2h+3))−(1/(2x+3))))/h) =lim_(h→0) (((((2x+3−2x−2h−3)/((2x+2h+3)(2x+3)))))/h) =lim_(h→0) (((((−2h)/((4x^2 +6x+4hx+6h+6x+9)))))/h) =lim_(h→0) (((((−2)/((4x^2 +6x+4hx+6h+6x+9)))))/1) =−(2/(4x^2 +12x+9)) =−(2/((2x+3)^2 ))
$$\left(\mathrm{2}\right) \\ $$$${f}\:'\left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}} \\ $$$${f}\:'\left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}}\right)−\left(\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{3}}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{3}}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{2}{x}+\mathrm{3}−\mathrm{2}{x}−\mathrm{2}{h}−\mathrm{3}}{\left(\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}\right)\left(\mathrm{2}{x}+\mathrm{3}\right)}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{−\mathrm{2}{h}}{\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{4}{hx}+\mathrm{6}{h}+\mathrm{6}{x}+\mathrm{9}\right)}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{−\mathrm{2}}{\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{4}{hx}+\mathrm{6}{h}+\mathrm{6}{x}+\mathrm{9}\right)}\right)}{\mathrm{1}} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{9}} \\ $$$$=−\frac{\mathrm{2}}{\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$
Answered by sandy_suhendra last updated on 06/Apr/17
3) lim_(h→0) ((sin2(x+h)−sin2x)/h) =lim_(h→0) ((2cos(2x+h) sin h)/h) =lim_(h→0) 2cos(2x+h) ((sin h)/h) =2cos(2x+0).1=2cos2x 4)lim_(h→0) ((cos2(x+h)−cos2x)/h) =lim_(x→0) ((−2sin(2x+h) sin h)/h) =lim_(x→0) −2sin(2x+h) ((sin h)/h) =−2sin(2x+0).1=−2sin2x
$$\left.\mathrm{3}\right)\:\mathrm{li}\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\mathrm{sin2}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{sin2x}}{\mathrm{h}} \\ $$$$=\mathrm{li}\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\mathrm{2cos}\left(\mathrm{2x}+\mathrm{h}\right)\:\mathrm{sin}\:\mathrm{h}}{\mathrm{h}} \\ $$$$=\mathrm{li}\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{m}}\:\mathrm{2cos}\left(\mathrm{2x}+\mathrm{h}\right)\:\frac{\mathrm{sin}\:\mathrm{h}}{\mathrm{h}} \\ $$$$=\mathrm{2cos}\left(\mathrm{2x}+\mathrm{0}\right).\mathrm{1}=\mathrm{2cos2x} \\ $$$$ \\ $$$$\left.\mathrm{4}\right)\mathrm{li}\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\mathrm{cos2}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{cos2x}}{\mathrm{h}} \\ $$$$=\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\:\frac{−\mathrm{2sin}\left(\mathrm{2x}+\mathrm{h}\right)\:\mathrm{sin}\:\mathrm{h}}{\mathrm{h}} \\ $$$$=\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\:−\mathrm{2sin}\left(\mathrm{2x}+\mathrm{h}\right)\:\frac{\mathrm{sin}\:\mathrm{h}}{\mathrm{h}} \\ $$$$=−\mathrm{2sin}\left(\mathrm{2x}+\mathrm{0}\right).\mathrm{1}=−\mathrm{2sin2x} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *