Question Number 132390 by bramlexs22 last updated on 14/Feb/21
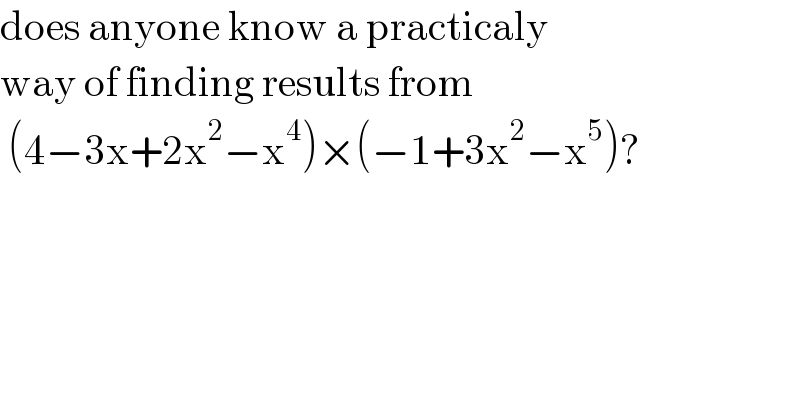
$$\mathrm{does}\:\mathrm{anyone}\:\mathrm{know}\:\mathrm{a}\:\mathrm{practicaly} \\ $$$$\mathrm{way}\:\mathrm{of}\:\mathrm{finding}\:\mathrm{results}\:\mathrm{from} \\ $$$$\:\left(\mathrm{4}−\mathrm{3x}+\mathrm{2x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{4}} \right)×\left(−\mathrm{1}+\mathrm{3x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{5}} \right)? \\ $$
Answered by EDWIN88 last updated on 14/Feb/21

$$\:\left(\mathrm{4}−\mathrm{3x}+\mathrm{2x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{4}} \right).\left(−\mathrm{1}+\mathrm{3x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{5}} \right)=? \\ $$$$\:\mathrm{solution}\:: \\ $$$$\:\begin{array}{|c|c|c|c|c|c|c|c|}{\:\:\:\mathrm{4}\:\:\:\:\:−\mathrm{3}\:\:\:\:\:\mathrm{2}\:\:\:\:\mathrm{0}\:\:\:\:\:−\mathrm{1}\:\:\:\:\:}\\{−\mathrm{1}\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:−\mathrm{1}}\\{×\:\:\:\:\:−\mathrm{4}\:\:\:\:\:\:\mathrm{3}\:\:\:−\mathrm{2}\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{1}}\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:}\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{12}\:\:\:−\mathrm{9}\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\:\mathrm{0}\:\:\:\:−\mathrm{3}}\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{0}\:\:\:\:\mathrm{0}\:\:\:\:\:}\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{4}\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:−\mathrm{2}\:\:\:\mathrm{0}\:\:\:\mathrm{1}}\\\hline\end{array} \\ $$$$\mathrm{the}\:\mathrm{result}\:\mathrm{is}\:−\mathrm{4}+\mathrm{3x}+\mathrm{10x}^{\mathrm{2}} −\mathrm{9x}^{\mathrm{3}} +\mathrm{6x}^{\mathrm{4}} −\mathrm{4x}^{\mathrm{5}} −\mathrm{2x}^{\mathrm{7}} +\mathrm{x}^{\mathrm{9}} \\ $$
Commented by bramlexs22 last updated on 14/Feb/21

$$\mathrm{waw}…..\mathrm{great} \\ $$
