Menu Close

dx-2cos-x-3sin-x-

Tinku Tara 0 Comments
Pin




Question Number 139776 by mohammad17 last updated on 01/May/21
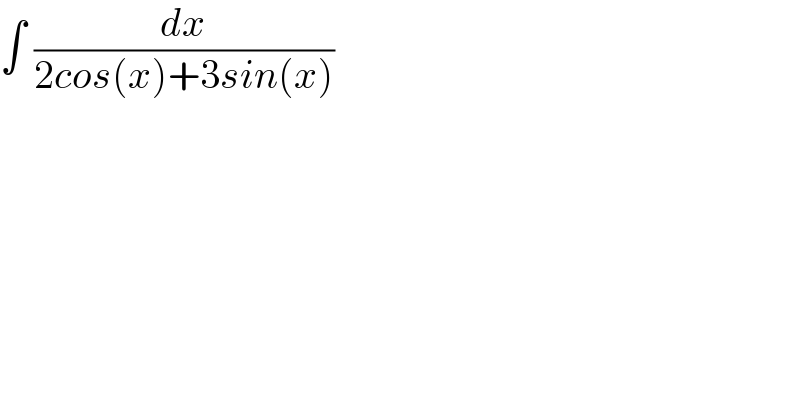
∫ (dx/(2cos(x)+3sin(x)))
$$\int\:\frac{{dx}}{\mathrm{2}{cos}\left({x}\right)+\mathrm{3}{sin}\left({x}\right)} \\ $$
Answered by phanphuoc last updated on 01/May/21
dx/rcos(x+α)
$${dx}/{rcos}\left({x}+\alpha\right) \\ $$
Answered by qaz last updated on 01/May/21
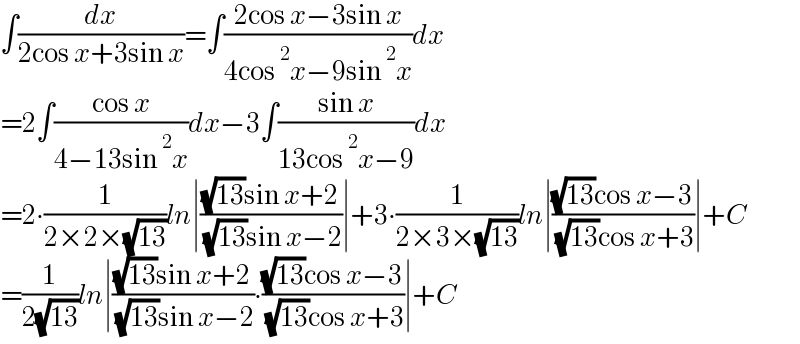
∫(dx/(2cos x+3sin x))=∫((2cos x−3sin x)/(4cos^2 x−9sin^2 x))dx =2∫((cos x)/(4−13sin^2 x))dx−3∫((sin x)/(13cos^2 x−9))dx =2∙(1/(2×2×(√(13))))ln∣(((√(13))sin x+2)/( (√(13))sin x−2))∣+3∙(1/(2×3×(√(13))))ln∣(((√(13))cos x−3)/( (√(13))cos x+3))∣+C =(1/(2(√(13))))ln∣(((√(13))sin x+2)/( (√(13))sin x−2))∙(((√(13))cos x−3)/( (√(13))cos x+3))∣+C
$$\int\frac{{dx}}{\mathrm{2cos}\:{x}+\mathrm{3sin}\:{x}}=\int\frac{\mathrm{2cos}\:{x}−\mathrm{3sin}\:{x}}{\mathrm{4cos}\:^{\mathrm{2}} {x}−\mathrm{9sin}\:^{\mathrm{2}} {x}}{dx} \\ $$$$=\mathrm{2}\int\frac{\mathrm{cos}\:{x}}{\mathrm{4}−\mathrm{13sin}\:^{\mathrm{2}} {x}}{dx}−\mathrm{3}\int\frac{\mathrm{sin}\:{x}}{\mathrm{13cos}\:^{\mathrm{2}} {x}−\mathrm{9}}{dx} \\ $$$$=\mathrm{2}\centerdot\frac{\mathrm{1}}{\mathrm{2}×\mathrm{2}×\sqrt{\mathrm{13}}}{ln}\mid\frac{\sqrt{\mathrm{13}}\mathrm{sin}\:{x}+\mathrm{2}}{\:\sqrt{\mathrm{13}}\mathrm{sin}\:{x}−\mathrm{2}}\mid+\mathrm{3}\centerdot\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}×\sqrt{\mathrm{13}}}{ln}\mid\frac{\sqrt{\mathrm{13}}\mathrm{cos}\:{x}−\mathrm{3}}{\:\sqrt{\mathrm{13}}\mathrm{cos}\:{x}+\mathrm{3}}\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{13}}}{ln}\mid\frac{\sqrt{\mathrm{13}}\mathrm{sin}\:{x}+\mathrm{2}}{\:\sqrt{\mathrm{13}}\mathrm{sin}\:{x}−\mathrm{2}}\centerdot\frac{\sqrt{\mathrm{13}}\mathrm{cos}\:{x}−\mathrm{3}}{\:\sqrt{\mathrm{13}}\mathrm{cos}\:{x}+\mathrm{3}}\mid+{C} \\ $$
Answered by Ankushkumarparcha last updated on 01/May/21
Solution: say I = ∫ (dx/(2cos(x)+3sin(x))) Using Weierstrass Substitution. I = ∫ (2/(2(((1−t^2 )/(1+t^2 )))+3(((2t)/(1+t^2 ))))) (dt/(1+t^2 )) => ∫ (dt/(1+3t−t^2 )) => −∫ (dt/((t − (3/2))^2 −(((√3)/2))^2 )) I = ∫ (dx/(2cos(x)+3sin(x))) = ((−1)/( (√(13)))) log∣((2tan(x/2)−3−(√(13)))/(2tan(x/2)−3+(√(13))))∣ +C
$${Solution}:\:{say}\:{I}\:=\:\int\:\frac{{dx}}{\mathrm{2cos}\left({x}\right)+\mathrm{3sin}\left({x}\right)}\: \\ $$$${Using}\:{Weierstrass}\:{Substitution}. \\ $$$${I}\:=\:\int\:\:\frac{\mathrm{2}}{\mathrm{2}\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)+\mathrm{3}\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)}\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=>\:\int\:\frac{{dt}}{\mathrm{1}+\mathrm{3}{t}−{t}^{\mathrm{2}} }\:=>\:−\int\:\frac{{dt}}{\left({t}\:−\:\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$${I}\:=\:\int\:\frac{{dx}}{\mathrm{2cos}\left({x}\right)+\mathrm{3sin}\left({x}\right)}\:=\:\frac{−\mathrm{1}}{\:\sqrt{\mathrm{13}}}\:\mathrm{log}\mid\frac{\mathrm{2tan}\left({x}/\mathrm{2}\right)−\mathrm{3}−\sqrt{\mathrm{13}}}{\mathrm{2tan}\left({x}/\mathrm{2}\right)−\mathrm{3}+\sqrt{\mathrm{13}}}\mid\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *