Question Number 142131 by Avijit007 last updated on 26/May/21
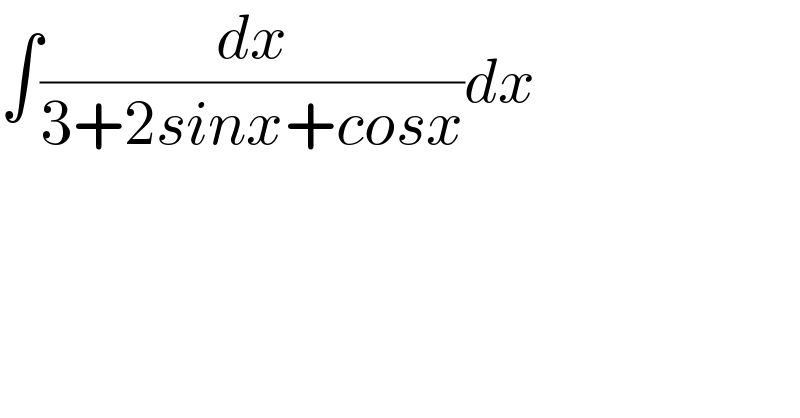
$$\int\frac{{dx}}{\mathrm{3}+\mathrm{2}{sinx}+{cosx}}{dx} \\ $$
Commented by Avijit007 last updated on 26/May/21

$${help} \\ $$
Answered by 676597498 last updated on 26/May/21
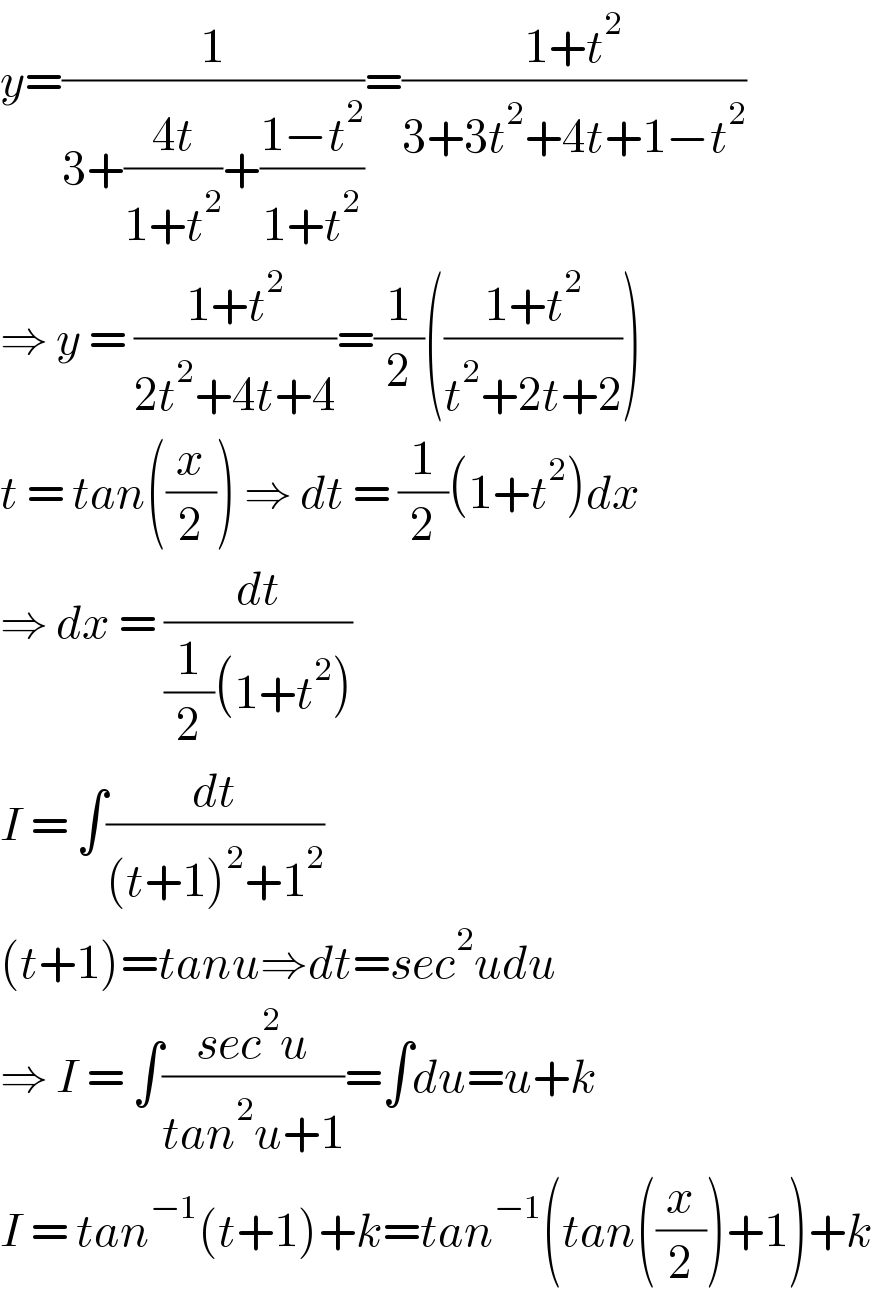
$${y}=\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{4}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}=\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{3}+\mathrm{3}{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{y}\:=\:\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}+{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{2}}\right) \\ $$$${t}\:=\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)\:\Rightarrow\:{dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dx} \\ $$$$\Rightarrow\:{dx}\:=\:\frac{{dt}}{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:\: \\ $$$${I}\:=\:\int\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} } \\ $$$$\left({t}+\mathrm{1}\right)={tanu}\Rightarrow{dt}={sec}^{\mathrm{2}} {udu} \\ $$$$\Rightarrow\:{I}\:=\:\int\frac{{sec}^{\mathrm{2}} {u}}{{tan}^{\mathrm{2}} {u}+\mathrm{1}}=\int{du}={u}+{k} \\ $$$${I}\:=\:{tan}^{−\mathrm{1}} \left({t}+\mathrm{1}\right)+{k}={tan}^{−\mathrm{1}} \left({tan}\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{1}\right)+{k} \\ $$
Commented by Avijit007 last updated on 26/May/21

$${thank}\:{you}\: \\ $$
