Menu Close

dx-5-4x-x-2-is-this-answer-correct-ln-1-4-x-5-ln6-1-x-C-

Tinku Tara 0 Comments
Pin




Question Number 11937 by tawa last updated on 05/Apr/17
∫(dx/( (√(5 + 4x − x^2 )))) is this answer correct ? −ln[1/4(x − 5) − ln6(− 1 − x)] + C
$$\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{5}\:+\:\mathrm{4x}\:−\:\mathrm{x}^{\mathrm{2}} }}\: \\ $$$$ \\ $$$$ \\ $$$$\mathrm{is}\:\mathrm{this}\:\mathrm{answer}\:\mathrm{correct}\:?\:\:\:\:\:\:\:\:\:\:\:−\mathrm{ln}\left[\mathrm{1}/\mathrm{4}\left(\mathrm{x}\:−\:\mathrm{5}\right)\:−\:\mathrm{ln6}\left(−\:\mathrm{1}\:−\:\mathrm{x}\right)\right]\:+\:\mathrm{C} \\ $$
Commented by ridwan balatif last updated on 06/Apr/17
∫(dx/( (√(5+4x−x^2 ))))=∫(dx/((9−(x−2)^2 )^(1/2) )) let: x−2=3sinθ x=3sinθ+2 (dx/dθ)=3cosθ dx=3cosθdθ ∫(dx/( (√(9−(x−2)^2 ))))=∫((3cosθ)/( (√(9−9sin^2 θ))))dθ =∫((3cosθ)/( (√(9(1−sin^2 θ)))))dθ =∫((3cosθ)/(3cosθ))dθ =θ+C from let: ((x−2)/3)=sinθ θ=sin^(−1) (((x−2)/3)) answer: sin^(−1) (((x−2)/3))+C
$$\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{5}+\mathrm{4x}−\mathrm{x}^{\mathrm{2}} }}=\int\frac{\mathrm{dx}}{\left(\mathrm{9}−\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$\mathrm{let}:\:\mathrm{x}−\mathrm{2}=\mathrm{3sin}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{x}=\mathrm{3sin}\theta+\mathrm{2} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{dx}}{\mathrm{d}\theta}=\mathrm{3cos}\theta \\ $$$$\:\:\:\:\:\:\mathrm{dx}=\mathrm{3cos}\theta\mathrm{d}\theta \\ $$$$\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{9}−\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }}=\int\frac{\mathrm{3cos}\theta}{\:\sqrt{\mathrm{9}−\mathrm{9sin}^{\mathrm{2}} \theta}}\mathrm{d}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int\frac{\mathrm{3cos}\theta}{\:\sqrt{\mathrm{9}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta\right)}}\mathrm{d}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int\frac{\mathrm{3cos}\theta}{\mathrm{3cos}\theta}\mathrm{d}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\theta+\mathrm{C} \\ $$$$\mathrm{from}\:\mathrm{let}: \\ $$$$\frac{\mathrm{x}−\mathrm{2}}{\mathrm{3}}=\mathrm{sin}\theta \\ $$$$\theta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{x}−\mathrm{2}}{\mathrm{3}}\right) \\ $$$$\mathrm{answer}:\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{x}−\mathrm{2}}{\mathrm{3}}\right)+\mathrm{C} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by ajfour last updated on 06/Apr/17
try differentiating your answer!
$${try}\:{differentiating}\:{your}\:{answer}! \\ $$
Commented by mrW1 last updated on 06/Apr/17
(dx/dθ)=3cos θ ⇒dx=3cos θdθ
$$\frac{{dx}}{{d}\theta}=\mathrm{3cos}\:\theta \\ $$$$\Rightarrow{dx}=\mathrm{3cos}\:\theta{d}\theta \\ $$
Commented by ridwan balatif last updated on 06/Apr/17
thank you sir, i have fixed it
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{have}\:\mathrm{fixed}\:\mathrm{it} \\ $$
Commented by tawa last updated on 07/Apr/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by ajfour last updated on 06/Apr/17
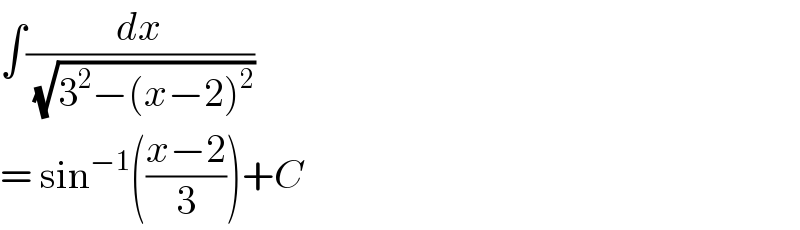
∫(dx/( (√(3^2 −(x−2)^2 )))) = sin^(−1) (((x−2)/3))+C
$$\int\frac{{dx}}{\:\sqrt{\mathrm{3}^{\mathrm{2}} −\left({x}−\mathrm{2}\right)^{\mathrm{2}} }} \\ $$$$=\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}−\mathrm{2}}{\mathrm{3}}\right)+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *