Question Number 76467 by kaivan.ahmadi last updated on 27/Dec/19
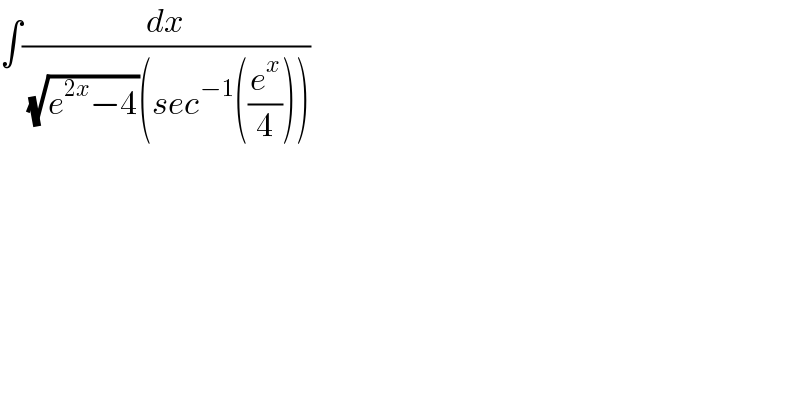
$$\int\frac{{dx}}{\:\sqrt{{e}^{\mathrm{2}{x}} −\mathrm{4}}\left({sec}^{−\mathrm{1}} \left(\frac{{e}^{{x}} }{\mathrm{4}}\right)\right)} \\ $$
Answered by john santu last updated on 28/Dec/19

$${let}\::\mathrm{sec}\:{u}\:=\:\frac{{e}^{{x}} }{\mathrm{4}}\:\rightarrow\:{e}^{{x}} \:{dx}=\mathrm{4sec}\:{u}\:×\mathrm{tan}\:{u}\:{du} \\ $$$${I}=\int\:\frac{\mathrm{4sec}\:{u}×\mathrm{tan}\:{udu}}{{e}^{{x}} \left(\sqrt{{e}^{\mathrm{2}{x}} −\mathrm{4}}\right)} \\ $$$$=\int\:\frac{\mathrm{4sec}\:{u}.\mathrm{tan}\:{u}\:{du}}{\mathrm{4sec}\:{u}\sqrt{\mathrm{16sec}\:^{\mathrm{2}} {u}−\mathrm{4}}} \\ $$$$\int\:\frac{\mathrm{tan}\:{u}\:{du}}{\mathrm{2}\sqrt{\mathrm{4sec}\:^{\mathrm{2}} {u}−\mathrm{1}}}\:=\:\int\:\frac{\mathrm{tan}\:{u}\:{du}}{\mathrm{2}\sqrt{\mathrm{4tan}\:^{\mathrm{2}} {u}+\mathrm{3}}} \\ $$$${now}\:{let}\:\mathrm{tan}\:{u}\:=\:\beta\: \\ $$
Commented by kaivan.ahmadi last updated on 29/Dec/19

$${thank}\:{you}\:{sir} \\ $$
