Question Number 141507 by I want to learn more last updated on 19/May/21
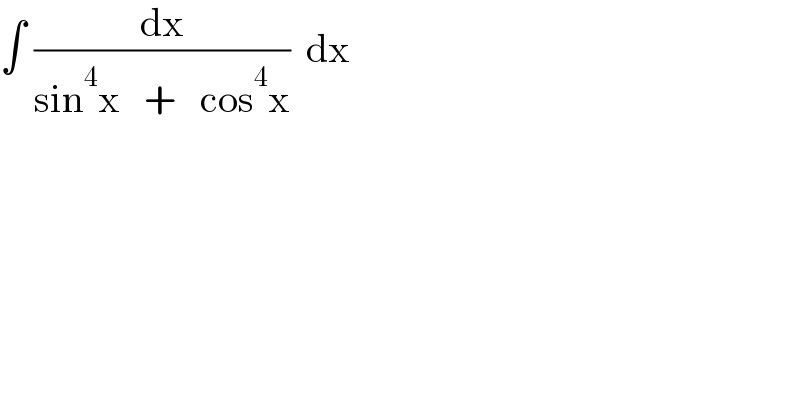
$$\int\:\frac{\mathrm{dx}}{\mathrm{sin}^{\mathrm{4}} \mathrm{x}\:\:\:+\:\:\:\mathrm{cos}^{\mathrm{4}} \mathrm{x}}\:\:\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 19/May/21

$$\Psi=\int\:\frac{\mathrm{dx}}{\mathrm{cos}^{\mathrm{4}} \mathrm{x}\:+\mathrm{sin}^{\mathrm{4}} \mathrm{x}}\:\Rightarrow\Psi=\int\:\frac{\mathrm{dx}}{\left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:+\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} −\mathrm{2cos}^{\mathrm{2}} \mathrm{x}.\mathrm{sin}^{\mathrm{2}} \mathrm{x}} \\ $$$$=\int\:\frac{\mathrm{dx}}{\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}}\right)^{\mathrm{2}} }\:=\int\:\frac{\mathrm{dx}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2x}\right)}=\int\:\frac{\mathrm{dx}}{\mathrm{1}−\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{4x}\right)}{\mathrm{4}}} \\ $$$$=\mathrm{4}\int\:\:\frac{\mathrm{dx}}{\mathrm{3}+\mathrm{cos}\left(\mathrm{4x}\right)}\:=_{\mathrm{4x}=\mathrm{t}} \:\:\int\:\:\frac{\mathrm{dt}}{\mathrm{3}+\mathrm{cost}}\:=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{y}} \:\:\int\:\:\frac{\mathrm{2dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)\left(\mathrm{3}+\frac{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }\right)} \\ $$$$=\int\:\:\frac{\mathrm{2dy}}{\mathrm{3y}^{\mathrm{2}} \:+\mathrm{3}+\mathrm{1}−\mathrm{y}^{\mathrm{2}} }\:=\int\:\frac{\mathrm{2dy}}{\mathrm{2y}^{\mathrm{2}} \:+\mathrm{4}}\:=\int\:\frac{\mathrm{dy}}{\mathrm{y}^{\mathrm{2}} \:+\mathrm{2}}\:=_{\mathrm{y}=\sqrt{\mathrm{2}}\mathrm{z}} \:\:\int\:\frac{\sqrt{\mathrm{2}}\mathrm{dz}}{\mathrm{2}\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\left(\mathrm{z}\right)\:+\mathrm{C}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\left(\frac{\mathrm{y}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{C}\:\Rightarrow \\ $$$$\Psi=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}\left(\mathrm{2x}\right)\right)\:+\mathrm{C} \\ $$
Commented by I want to learn more last updated on 19/May/21
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate} \\ $$
Answered by peter frank last updated on 19/May/21
Answered by peter frank last updated on 19/May/21
Commented by I want to learn more last updated on 19/May/21
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by I want to learn more last updated on 19/May/21
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by Rozix last updated on 20/May/21
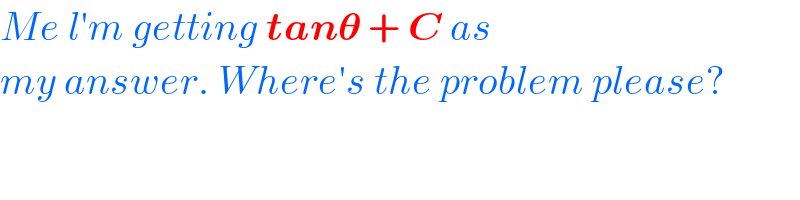
$${Me}\:{l}'{m}\:{getting}\:\boldsymbol{{tan}\theta}\:+\:\boldsymbol{{C}}\:{as} \\ $$$${my}\:{answer}.\:{Where}'{s}\:{the}\:{problem}\:{please}? \\ $$
Commented by mathmax by abdo last updated on 20/May/21

$$\mathrm{not}\:\mathrm{correct}\:\mathrm{chow}\:\mathrm{your}\:\mathrm{work}\:\mathrm{sir} \\ $$
