Question Number 136440 by liberty last updated on 22/Mar/21

$$\:\int\:\frac{{dx}}{\mathrm{sin}\:^{\mathrm{6}} {x}}\:? \\ $$
Answered by rs4089 last updated on 22/Mar/21
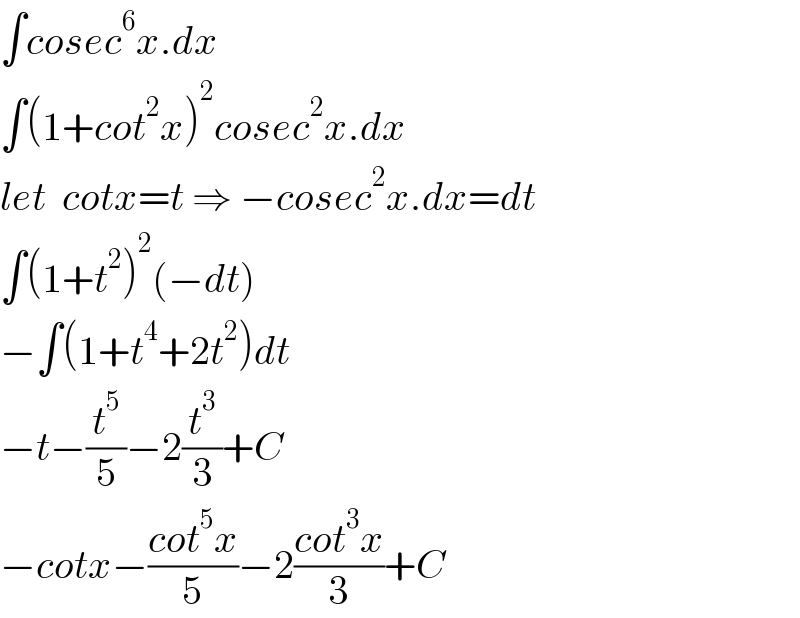
$$\int{cosec}^{\mathrm{6}} {x}.{dx} \\ $$$$\int\left(\mathrm{1}+{cot}^{\mathrm{2}} {x}\right)^{\mathrm{2}} {cosec}^{\mathrm{2}} {x}.{dx} \\ $$$${let}\:\:{cotx}={t}\:\Rightarrow\:−{cosec}^{\mathrm{2}} {x}.{dx}={dt} \\ $$$$\int\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \left(−{dt}\right) \\ $$$$−\int\left(\mathrm{1}+{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} \right){dt} \\ $$$$−{t}−\frac{{t}^{\mathrm{5}} }{\mathrm{5}}−\mathrm{2}\frac{{t}^{\mathrm{3}} }{\mathrm{3}}+{C} \\ $$$$−{cotx}−\frac{{cot}^{\mathrm{5}} {x}}{\mathrm{5}}−\mathrm{2}\frac{{cot}^{\mathrm{3}} {x}}{\mathrm{3}}+{C} \\ $$
Answered by EDWIN88 last updated on 22/Mar/21
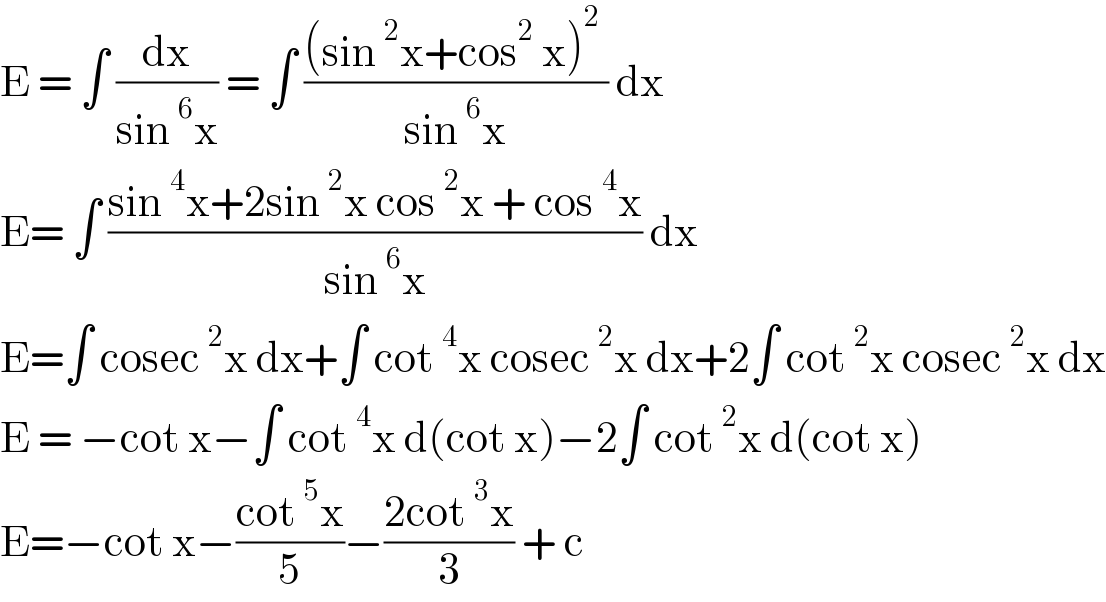
$$\mathrm{E}\:=\:\int\:\frac{\mathrm{dx}}{\mathrm{sin}\:^{\mathrm{6}} \mathrm{x}}\:=\:\int\:\frac{\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \:\mathrm{x}\right)^{\mathrm{2}} \:}{\mathrm{sin}\:^{\mathrm{6}} \mathrm{x}}\:\mathrm{dx} \\ $$$$\mathrm{E}=\:\int\:\frac{\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}+\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:+\:\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}}{\mathrm{sin}\:^{\mathrm{6}} \mathrm{x}}\:\mathrm{dx} \\ $$$$\mathrm{E}=\int\:\mathrm{cosec}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}+\int\:\mathrm{cot}\:^{\mathrm{4}} \mathrm{x}\:\mathrm{cosec}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}+\mathrm{2}\int\:\mathrm{cot}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{cosec}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$\mathrm{E}\:=\:−\mathrm{cot}\:\mathrm{x}−\int\:\mathrm{cot}\:^{\mathrm{4}} \mathrm{x}\:\mathrm{d}\left(\mathrm{cot}\:\mathrm{x}\right)−\mathrm{2}\int\:\mathrm{cot}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{d}\left(\mathrm{cot}\:\mathrm{x}\right) \\ $$$$\mathrm{E}=−\mathrm{cot}\:\mathrm{x}−\frac{\mathrm{cot}\:^{\mathrm{5}} \mathrm{x}}{\mathrm{5}}−\frac{\mathrm{2cot}\:^{\mathrm{3}} \mathrm{x}}{\mathrm{3}}\:+\:\mathrm{c}\: \\ $$
