Question Number 137279 by Ñï= last updated on 31/Mar/21
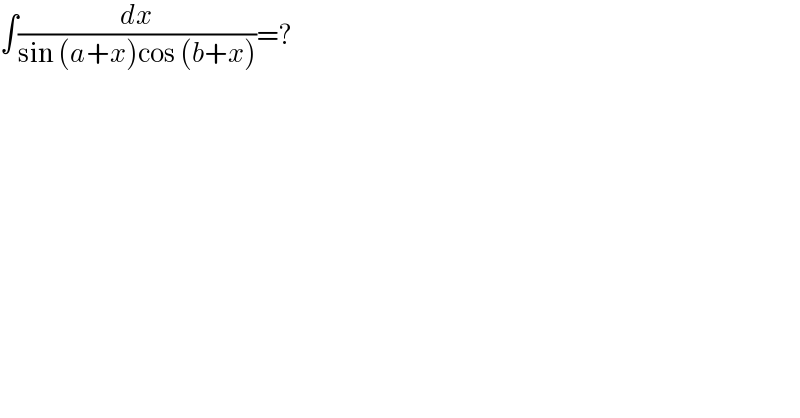
$$\int\frac{{dx}}{\mathrm{sin}\:\left({a}+{x}\right)\mathrm{cos}\:\left({b}+{x}\right)}=? \\ $$
Answered by Ar Brandon last updated on 31/Mar/21
![I=∫(dx/(sin(a+x)cos(b+x))) =(1/(cos(a−b)))∫((cos(a−b))/(sin(a+x)cos(b+x)))dx =(1/(cos(a−b)))∫((cos[(x+a)−(x+b)])/(sin(a+x)cos(b+x)))dx =(1/(cos(a−b)))∫((cos(x+a)cos(x+b)+sin(x+a)sin(x+b))/(sin(a+x)cos(b+x)))dx =(1/(cos(a−b)))∫{cot(a+x)+tan(b+x}dx =(1/(cos(a−b))){ln∣sin(a+x)∣−ln∣cos(b+x)∣}+C](https://www.tinkutara.com/question/Q137291.png)
$$\mathcal{I}=\int\frac{\mathrm{dx}}{\mathrm{sin}\left(\mathrm{a}+\mathrm{x}\right)\mathrm{cos}\left(\mathrm{b}+\mathrm{x}\right)} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{cos}\left(\mathrm{a}−\mathrm{b}\right)}\int\frac{\mathrm{cos}\left(\mathrm{a}−\mathrm{b}\right)}{\mathrm{sin}\left(\mathrm{a}+\mathrm{x}\right)\mathrm{cos}\left(\mathrm{b}+\mathrm{x}\right)}\mathrm{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{cos}\left(\mathrm{a}−\mathrm{b}\right)}\int\frac{\mathrm{cos}\left[\left(\mathrm{x}+\mathrm{a}\right)−\left(\mathrm{x}+\mathrm{b}\right)\right]}{\mathrm{sin}\left(\mathrm{a}+\mathrm{x}\right)\mathrm{cos}\left(\mathrm{b}+\mathrm{x}\right)}\mathrm{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{cos}\left(\mathrm{a}−\mathrm{b}\right)}\int\frac{\mathrm{cos}\left(\mathrm{x}+\mathrm{a}\right)\mathrm{cos}\left(\mathrm{x}+\mathrm{b}\right)+\mathrm{sin}\left(\mathrm{x}+\mathrm{a}\right)\mathrm{sin}\left(\mathrm{x}+\mathrm{b}\right)}{\mathrm{sin}\left(\mathrm{a}+\mathrm{x}\right)\mathrm{cos}\left(\mathrm{b}+\mathrm{x}\right)}\mathrm{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{cos}\left(\mathrm{a}−\mathrm{b}\right)}\int\left\{\mathrm{cot}\left(\mathrm{a}+\mathrm{x}\right)+\mathrm{tan}\left(\mathrm{b}+\mathrm{x}\right\}\mathrm{dx}\right. \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{cos}\left(\mathrm{a}−\mathrm{b}\right)}\left\{\mathrm{ln}\mid\mathrm{sin}\left(\mathrm{a}+\mathrm{x}\right)\mid−\mathrm{ln}\mid\mathrm{cos}\left(\mathrm{b}+\mathrm{x}\right)\mid\right\}+\mathcal{C} \\ $$
Commented by Ñï= last updated on 31/Mar/21

$${cool}!!! \\ $$
