Menu Close

dx-sin-x-cos-x-

Tinku Tara 0 Comments
Pin




Question Number 136365 by liberty last updated on 21/Mar/21
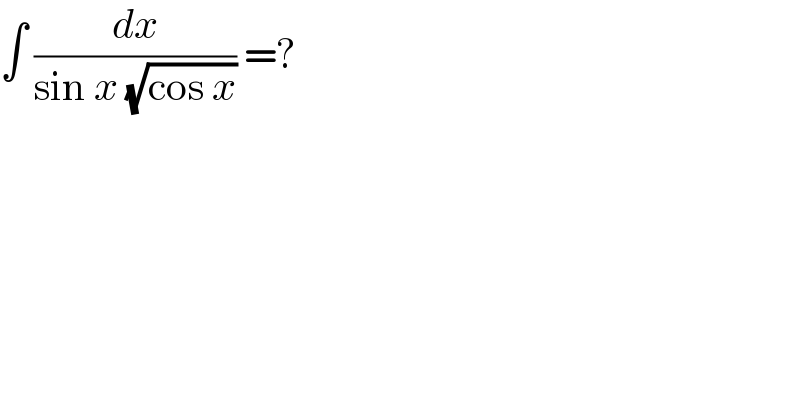
∫ (dx/(sin x (√(cos x)))) =?
$$\int\:\frac{{dx}}{\mathrm{sin}\:{x}\:\sqrt{\mathrm{cos}\:{x}}}\:=? \\ $$
Answered by mathmax by abdo last updated on 21/Mar/21
I =∫ (dx/(sinx(√(cosx)))) we do the changement cosx=t^2 ⇒x=arcos(t^2 ) ⇒sinx=(√(1−t^4 )) ⇒I =∫ ((−2t)/( (√(1−t^4 )).(√(1−t^4 ))t))dt =−2∫ (dt/(1−t^4 )) =2∫ (dt/(t^4 −1)) let decompose F(t)=(1/(t^4 −1)) ⇒F(t)=(1/((t^2 −1)(t^2 +1))) =(1/((t−1)(t+1)(t^2 +1)))=(a/(t−1))+(b/(t+1)) +((nt+m)/(t^2 +1)) a=(1/4) ,b=−(1/4) , lim_(t→+∞) tF(t)=0 =a+b+n ⇒n=0 F(o)=−1=−a+b +m ⇒m=−1+a−b =−1+(1/2)=−(1/2) ⇒ F(t)=(1/(4(t−1)))−(1/(4(t+1)))−(1/(2(t^2 +1))) ⇒ I =−2∫ F(t)dt =−2{(1/4)ln∣((t−1)/(t+1))∣−(1/2) arctan(t)} +C =−(1/2)ln∣((t−1)/(t+1))∣+arctan(t) +C =arctan((√(cosx)))−(1/2)ln∣(((√(cosx))−1)/( (√(cosx))+1))∣ +C
$$\mathrm{I}\:=\int\:\frac{\mathrm{dx}}{\mathrm{sinx}\sqrt{\mathrm{cosx}}}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{cosx}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}=\mathrm{arcos}\left(\mathrm{t}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{sinx}=\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{4}} }\:\Rightarrow\mathrm{I}\:=\int\:\:\:\frac{−\mathrm{2t}}{\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{4}} }.\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{4}} }\mathrm{t}}\mathrm{dt}\:=−\mathrm{2}\int\:\:\:\frac{\mathrm{dt}}{\mathrm{1}−\mathrm{t}^{\mathrm{4}} } \\ $$$$=\mathrm{2}\int\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{4}} −\mathrm{1}}\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{4}} −\mathrm{1}}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{t}−\mathrm{1}\right)\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{\mathrm{a}}{\mathrm{t}−\mathrm{1}}+\frac{\mathrm{b}}{\mathrm{t}+\mathrm{1}}\:+\frac{\mathrm{nt}+\mathrm{m}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{a}=\frac{\mathrm{1}}{\mathrm{4}}\:,\mathrm{b}=−\frac{\mathrm{1}}{\mathrm{4}}\:\:,\:\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)=\mathrm{0}\:=\mathrm{a}+\mathrm{b}+\mathrm{n}\:\Rightarrow\mathrm{n}=\mathrm{0} \\ $$$$\mathrm{F}\left(\mathrm{o}\right)=−\mathrm{1}=−\mathrm{a}+\mathrm{b}\:+\mathrm{m}\:\Rightarrow\mathrm{m}=−\mathrm{1}+\mathrm{a}−\mathrm{b}\:=−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{t}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{t}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\mathrm{I}\:=−\mathrm{2}\int\:\mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}\:=−\mathrm{2}\left\{\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}\mid−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{arctan}\left(\mathrm{t}\right)\right\}\:+\mathrm{C} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}\mid+\mathrm{arctan}\left(\mathrm{t}\right)\:+\mathrm{C} \\ $$$$=\mathrm{arctan}\left(\sqrt{\mathrm{cosx}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{cosx}}−\mathrm{1}}{\:\sqrt{\mathrm{cosx}}+\mathrm{1}}\mid\:+\mathrm{C} \\ $$
Answered by EDWIN88 last updated on 21/Mar/21
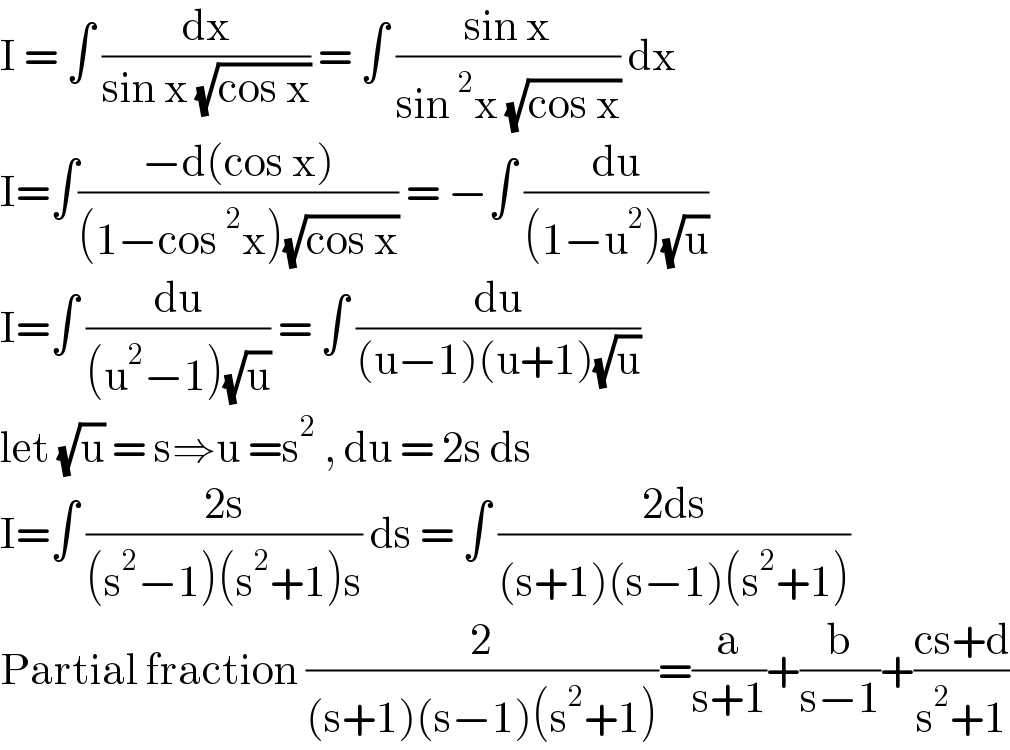
I = ∫ (dx/(sin x (√(cos x)))) = ∫ ((sin x)/(sin^2 x (√(cos x)))) dx I=∫((−d(cos x))/((1−cos^2 x)(√(cos x)))) = −∫ (du/((1−u^2 )(√u))) I=∫ (du/((u^2 −1)(√u))) = ∫ (du/((u−1)(u+1)(√u))) let (√u) = s⇒u =s^2 , du = 2s ds I=∫ ((2s)/((s^2 −1)(s^2 +1)s)) ds = ∫ ((2ds)/((s+1)(s−1)(s^2 +1))) Partial fraction (2/((s+1)(s−1)(s^2 +1)))=(a/(s+1))+(b/(s−1))+((cs+d)/(s^2 +1))
$$\mathrm{I}\:=\:\int\:\frac{\mathrm{dx}}{\mathrm{sin}\:\mathrm{x}\:\sqrt{\mathrm{cos}\:\mathrm{x}}}\:=\:\int\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\:\sqrt{\mathrm{cos}\:\mathrm{x}}}\:\mathrm{dx} \\ $$$$\mathrm{I}=\int\frac{−\mathrm{d}\left(\mathrm{cos}\:\mathrm{x}\right)}{\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\right)\sqrt{\mathrm{cos}\:\mathrm{x}}}\:=\:−\int\:\frac{\mathrm{du}}{\left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)\sqrt{\mathrm{u}}} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{du}}{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{u}}}\:=\:\int\:\frac{\mathrm{du}}{\left(\mathrm{u}−\mathrm{1}\right)\left(\mathrm{u}+\mathrm{1}\right)\sqrt{\mathrm{u}}} \\ $$$$\mathrm{let}\:\sqrt{\mathrm{u}}\:=\:\mathrm{s}\Rightarrow\mathrm{u}\:=\mathrm{s}^{\mathrm{2}} \:,\:\mathrm{du}\:=\:\mathrm{2s}\:\mathrm{ds} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{2s}}{\left(\mathrm{s}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{s}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{s}}\:\mathrm{ds}\:=\:\int\:\frac{\mathrm{2ds}}{\left(\mathrm{s}+\mathrm{1}\right)\left(\mathrm{s}−\mathrm{1}\right)\left(\mathrm{s}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\mathrm{Partial}\:\mathrm{fraction}\:\frac{\mathrm{2}}{\left(\mathrm{s}+\mathrm{1}\right)\left(\mathrm{s}−\mathrm{1}\right)\left(\mathrm{s}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{\mathrm{a}}{\mathrm{s}+\mathrm{1}}+\frac{\mathrm{b}}{\mathrm{s}−\mathrm{1}}+\frac{\mathrm{cs}+\mathrm{d}}{\mathrm{s}^{\mathrm{2}} +\mathrm{1}} \\ $$
Answered by mindispower last updated on 21/Mar/21
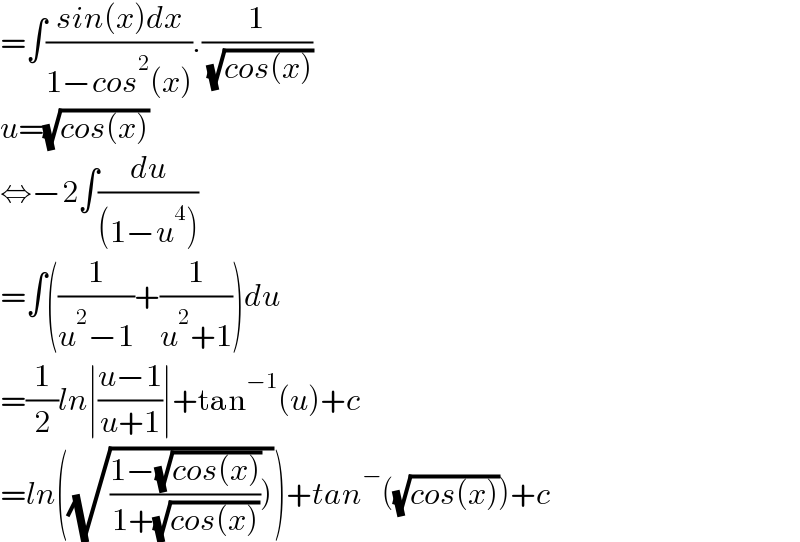
=∫((sin(x)dx)/(1−cos^2 (x))).(1/( (√(cos(x))))) u=(√(cos(x))) ⇔−2∫(du/((1−u^4 ))) =∫((1/(u^2 −1))+(1/(u^2 +1)))du =(1/2)ln∣((u−1)/(u+1))∣+tan^(−1) (u)+c =ln((√(((1−(√(cos(x))))/(1+(√(cos(x)))))))))+tan^− ((√(cos(x))))+c
$$=\int\frac{{sin}\left({x}\right){dx}}{\mathrm{1}−{cos}^{\mathrm{2}} \left({x}\right)}.\frac{\mathrm{1}}{\:\sqrt{{cos}\left({x}\right)}} \\ $$$${u}=\sqrt{{cos}\left({x}\right)} \\ $$$$\Leftrightarrow−\mathrm{2}\int\frac{{du}}{\left(\mathrm{1}−{u}^{\mathrm{4}} \right)} \\ $$$$=\int\left(\frac{\mathrm{1}}{{u}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid+\mathrm{tan}^{−\mathrm{1}} \left({u}\right)+{c} \\ $$$$={ln}\left(\sqrt{\left.\frac{\mathrm{1}−\sqrt{{cos}\left({x}\right)}}{\mathrm{1}+\sqrt{{cos}\left({x}\right)}}\right)}\right)+{tan}^{−} \left(\sqrt{{cos}\left({x}\right)}\right)+{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *