dx-sinx-cosx-

Facebook Tweet Pin

Question Number 141753 by mohammad17 last updated on 23/May/21

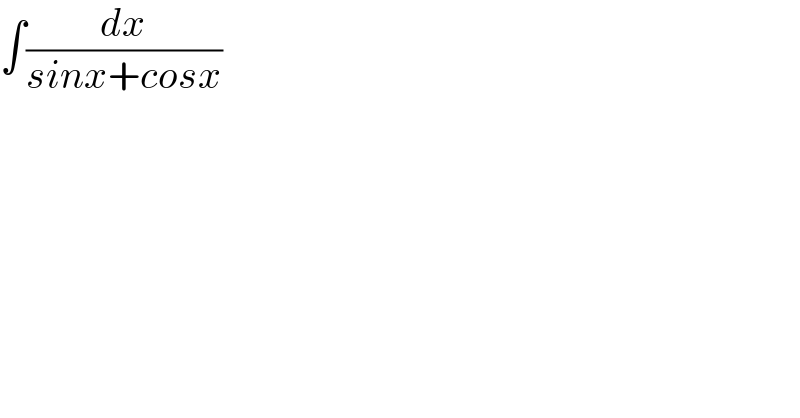
$$\int\frac{{dx}}{{sinx}+{cosx}} \\ $$

Commented by mohammad17 last updated on 23/May/21

$${help}\:{me}\:{sir} \\ $$

Answered by rs4089 last updated on 23/May/21

(1/( (√2)))∫(dx/(sin(x+(π/4))))=(1/( (√2)))∫cosec(x+(π/4)) (1/( (√2)))log_e [cosec(x+(π/4))−cot(x+(π/4))]+C

$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{dx}}{{sin}\left({x}+\frac{\pi}{\mathrm{4}}\right)}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int{cosec}\left({x}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{log}_{{e}} \left[{cosec}\left({x}+\frac{\pi}{\mathrm{4}}\right)−{cot}\left({x}+\frac{\pi}{\mathrm{4}}\right)\right]+{C} \\ $$

Commented by mohammad17 last updated on 23/May/21

Commented by mohammad17 last updated on 23/May/21

$${sir}\:{this}\:{answer}\:{is}\:{true}\:{or}\:{false}\:? \\ $$

Commented by mohammad17 last updated on 23/May/21

i think out the integral is (1/( (√2))) not (√2)

$${i}\:{think}\:{out}\:{the}\:{integral}\:{is}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{not}\:\sqrt{\mathrm{2}} \\ $$

Commented by rs4089 last updated on 23/May/21

$${yes}\:{sir}\:,\:{you}\:{are}\:{right}\:, \\ $$$$\:{thank}\:{you}\:{very}\:{much} \\ $$

Answered by mathmax by abdo last updated on 23/May/21

I=∫ (dx/(sinx +cosx)) we do the changement tan((x/2))=y ⇒ I =∫ ((2dy)/((1+y^2 )(((2y)/(1+y^2 ))+((1−y^2 )/(1+y^2 ))))) =∫ ((2dy)/(2y+1−y^2 )) =−2∫ (dy/(y^2 −2y−1)) =−2 ∫ (dy/((y−1)^2 −2)) =_(y−1=(√2)t) −2 ∫ (((√2)dt)/(2(t^2 −1))) =−(√2)∫ (dt/(t^2 −1))=−(1/( (√2)))∫ ((1/(t−1))−(1/(t+1)))dt =(1/( (√2)))log∣((t+1)/(t−1))∣ +C =(1/( (√2)))log∣((((y−1)/( (√2)))+1)/(((y−1)/( (√2)))−1))∣ +C ⇒ I=(1/( (√2)))log∣((tan((x/2))−1+(√2))/(tan((x/2))−1−(√2)))∣ +C

$$\mathrm{I}=\int\:\:\frac{\mathrm{dx}}{\mathrm{sinx}\:+\mathrm{cosx}}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{y}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\:\frac{\mathrm{2dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)\left(\frac{\mathrm{2y}}{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }+\frac{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }\right)}\:=\int\:\frac{\mathrm{2dy}}{\mathrm{2y}+\mathrm{1}−\mathrm{y}^{\mathrm{2}} } \\ $$$$=−\mathrm{2}\int\:\:\frac{\mathrm{dy}}{\mathrm{y}^{\mathrm{2}} −\mathrm{2y}−\mathrm{1}}\:=−\mathrm{2}\:\int\:\:\frac{\mathrm{dy}}{\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$=_{\mathrm{y}−\mathrm{1}=\sqrt{\mathrm{2}}\mathrm{t}} \:\:\:−\mathrm{2}\:\int\:\frac{\sqrt{\mathrm{2}}\mathrm{dt}}{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)}\:=−\sqrt{\mathrm{2}}\int\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\:\left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{log}\mid\frac{\mathrm{t}+\mathrm{1}}{\mathrm{t}−\mathrm{1}}\mid\:+\mathrm{C}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{log}\mid\frac{\frac{\mathrm{y}−\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\mathrm{1}}{\frac{\mathrm{y}−\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\mathrm{1}}\mid\:+\mathrm{C}\:\Rightarrow \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{log}\mid\frac{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{1}−\sqrt{\mathrm{2}}}\mid\:+\mathrm{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply