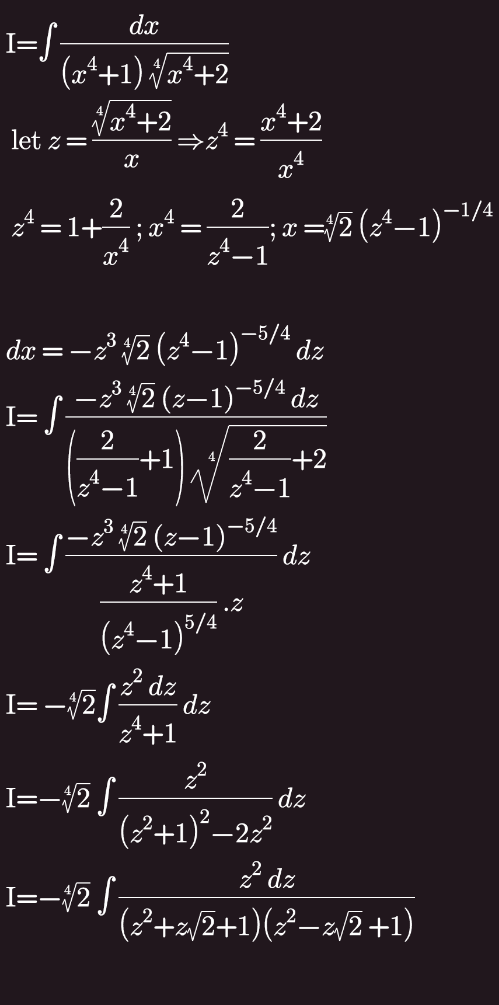Question Number 133109 by EDWIN88 last updated on 18/Feb/21
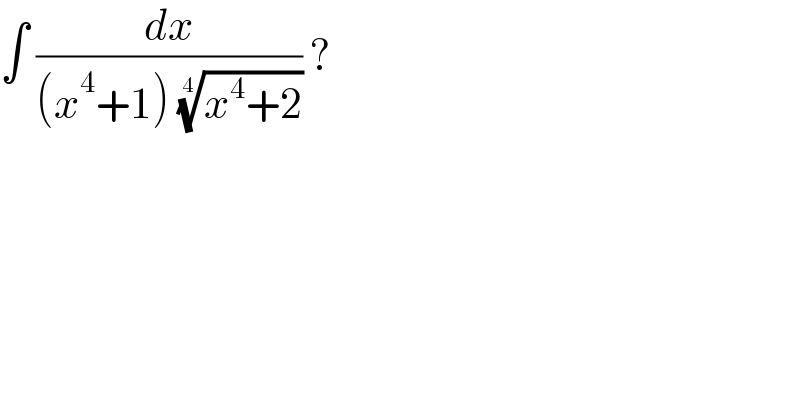
$$\int\:\frac{{dx}}{\left({x}^{\mathrm{4}} +\mathrm{1}\right)\:\sqrt[{\mathrm{4}}]{{x}^{\mathrm{4}} +\mathrm{2}}}\:? \\ $$
Commented by liberty last updated on 20/Feb/21
![I = ∫ (dx/((x^4 +1) ((x^4 +2))^(1/4) )) I=∫ (((1/x^5 ) dx)/((1+(1/x^4 )) ((1+(2/x^4 )))^(1/4) )) I=−(1/4)∫ ((d((1/x^4 )))/((1+(1/x^4 )) ((1+(2/x^4 )))^(1/4) )) let (1/x^4 ) = y I=−(1/4)∫ (dy/((1+y)((1+2y))^(1/4) )) let again z = ((1+2y))^(1/4) ; y=((z^4 −1)/2) I=−(1/4)∫ ((2z^3 dz)/((1+((z^4 −1)/2))z)) I=−∫ (z^2 /(z^4 +1)) dz =−∫ (1/(z^2 +(1/z^2 ))) dz I=−(1/2)∫ (((1+(1/z^2 ))+(1−(1/z^2 )))/(z^2 +(1/z^2 ))) dz I=−(1/2)[∫ ((d(z−(1/z)))/((z−(1/z))^2 +2))+ ∫ ((d(z+(1/z)))/((z+(1/z))^2 −2)) ] I=−(1/2)[ (1/( (√2))) arctan(((z−(1/z))/( (√2))))+(1/(2(√2))) ln ∣((z+(1/z)−(√2))/(z+(1/z)+(√2)))∣ + c I=−(1/(2(√2))) arctan (((z^2 −1)/(z(√2))))−(1/(4(√2)))ln ∣((z^2 −z(√2)+1)/(z^2 +z(√2)+1))∣+c I=−(1/(2(√2)))arctan ((((√(1+2y))−1)/( (√2) ((1+2y))^(1/4) )))−(1/(4(√2)))ln ∣(((√(1+2y))−(√2) ((1+2y))^(1/4) +1)/( (√(1+2y))+(√2) ((1+2y))^(1/4) +1))∣ + c I= −(1/(2(√2)))arctan (((x^2 (√(x^4 +2))−1)/(x(√2) ((x^4 +2))^(1/4) )))−(1/(4(√2)))ln ∣((x^2 (√(x^4 +2)) −x(√2) (√(x^4 +2)) +1)/(x^2 (√(x^4 +2)) +x(√2) ((x^4 +2))^(1/4) +1))∣+c](https://www.tinkutara.com/question/Q133235.png)
$$\mathrm{I}\:=\:\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)\:\sqrt[{\mathrm{4}}]{\mathrm{x}^{\mathrm{4}} +\mathrm{2}}} \\ $$$$\mathrm{I}=\int\:\frac{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{5}} }\:\mathrm{dx}}{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }\right)\:\sqrt[{\mathrm{4}}]{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{4}} }}} \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{d}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }\right)}{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }\right)\:\sqrt[{\mathrm{4}}]{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{4}} }}} \\ $$$$\:\mathrm{let}\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }\:=\:\mathrm{y} \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{dy}}{\left(\mathrm{1}+\mathrm{y}\right)\sqrt[{\mathrm{4}}]{\mathrm{1}+\mathrm{2y}}} \\ $$$$\mathrm{let}\:\mathrm{again}\:\mathrm{z}\:=\:\sqrt[{\mathrm{4}}]{\mathrm{1}+\mathrm{2y}}\:;\:\mathrm{y}=\frac{\mathrm{z}^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{2z}^{\mathrm{3}} \:\mathrm{dz}}{\left(\mathrm{1}+\frac{\mathrm{z}^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}}\right)\mathrm{z}} \\ $$$$\mathrm{I}=−\int\:\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{z}^{\mathrm{4}} +\mathrm{1}}\:\mathrm{dz}\:=−\int\:\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }}\:\mathrm{dz} \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }\right)+\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }\right)}{\mathrm{z}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }}\:\mathrm{dz} \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{2}}\left[\int\:\frac{\mathrm{d}\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{z}}\right)}{\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{z}}\right)^{\mathrm{2}} +\mathrm{2}}+\:\int\:\frac{\mathrm{d}\left(\mathrm{z}+\frac{\mathrm{1}}{\mathrm{z}}\right)}{\left(\mathrm{z}+\frac{\mathrm{1}}{\mathrm{z}}\right)^{\mathrm{2}} −\mathrm{2}}\:\right] \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{2}}\left[\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{arctan}\left(\frac{\mathrm{z}−\frac{\mathrm{1}}{\mathrm{z}}}{\:\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\mathrm{ln}\:\mid\frac{\mathrm{z}+\frac{\mathrm{1}}{\mathrm{z}}−\sqrt{\mathrm{2}}}{\mathrm{z}+\frac{\mathrm{1}}{\mathrm{z}}+\sqrt{\mathrm{2}}}\mid\:+\:\mathrm{c}\:\right. \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\mathrm{arctan}\:\left(\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{1}}{\mathrm{z}\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{ln}\:\mid\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{z}\sqrt{\mathrm{2}}+\mathrm{1}}{\mathrm{z}^{\mathrm{2}} +\mathrm{z}\sqrt{\mathrm{2}}+\mathrm{1}}\mid+\mathrm{c} \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{arctan}\:\left(\frac{\sqrt{\mathrm{1}+\mathrm{2y}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}\:\sqrt[{\mathrm{4}}]{\mathrm{1}+\mathrm{2y}}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{1}+\mathrm{2y}}−\sqrt{\mathrm{2}}\:\sqrt[{\mathrm{4}}]{\mathrm{1}+\mathrm{2y}}\:+\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{2y}}+\sqrt{\mathrm{2}}\:\sqrt[{\mathrm{4}}]{\mathrm{1}+\mathrm{2y}}\:+\mathrm{1}}\mid\:+\:\mathrm{c} \\ $$$$\mathrm{I}=\:−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{arctan}\:\left(\frac{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{2}}−\mathrm{1}}{\mathrm{x}\sqrt{\mathrm{2}}\:\sqrt[{\mathrm{4}}]{\mathrm{x}^{\mathrm{4}} +\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{ln}\:\mid\frac{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{2}}\:−\mathrm{x}\sqrt{\mathrm{2}}\:\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{2}}\:+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{2}}\:+\mathrm{x}\sqrt{\mathrm{2}}\:\sqrt[{\mathrm{4}}]{\mathrm{x}^{\mathrm{4}} +\mathrm{2}}\:+\mathrm{1}}\mid+\mathrm{c}\: \\ $$$$ \\ $$
Answered by MJS_new last updated on 19/Feb/21
![∫(dx/((x^4 +1)((x^4 +2))^(1/4) ))= [t=(((x^4 +2))^(1/4) /x) ⇔ x=((2/(t^4 −1)))^(1/4) → dx=−((x^2 (((x^2 +2)^3 ))^(1/4) )/2)dt] =−∫(t^2 /(t^4 +1))dt and this should be “easy”](https://www.tinkutara.com/question/Q133174.png)
$$\int\frac{{dx}}{\left({x}^{\mathrm{4}} +\mathrm{1}\right)\sqrt[{\mathrm{4}}]{{x}^{\mathrm{4}} +\mathrm{2}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt[{\mathrm{4}}]{{x}^{\mathrm{4}} +\mathrm{2}}}{{x}}\:\Leftrightarrow\:{x}=\sqrt[{\mathrm{4}}]{\frac{\mathrm{2}}{{t}^{\mathrm{4}} −\mathrm{1}}}\:\rightarrow\:{dx}=−\frac{{x}^{\mathrm{2}} \sqrt[{\mathrm{4}}]{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} }}{\mathrm{2}}{dt}\right] \\ $$$$=−\int\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} +\mathrm{1}}{dt} \\ $$$$\mathrm{and}\:\mathrm{this}\:\mathrm{should}\:\mathrm{be}\:“\mathrm{easy}'' \\ $$
Answered by john_santu last updated on 19/Feb/21