Menu Close

dy-1-y-2-tan-1-y-c-why-and-dy-1-y-2-

Tinku Tara 0 Comments
Pin




Question Number 5100 by LMTV last updated on 12/Apr/16
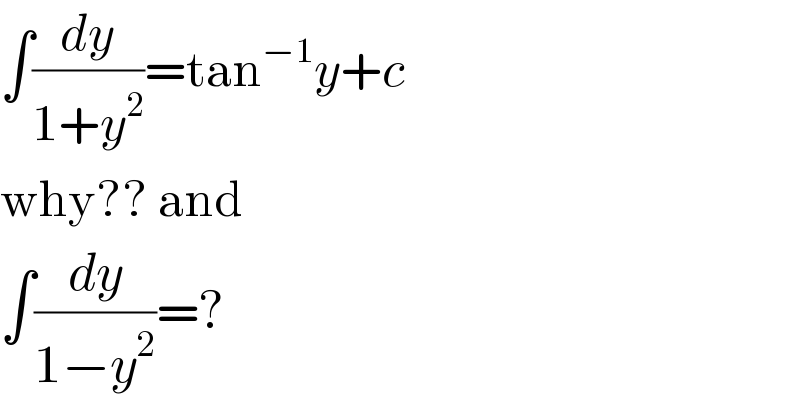
∫(dy/(1+y^2 ))=tan^(−1) y+c why?? and ∫(dy/(1−y^2 ))=?
$$\int\frac{{dy}}{\mathrm{1}+{y}^{\mathrm{2}} }=\mathrm{tan}^{−\mathrm{1}} {y}+{c} \\ $$$$\mathrm{why}??\:\mathrm{and} \\ $$$$\int\frac{{dy}}{\mathrm{1}−{y}^{\mathrm{2}} }=? \\ $$
Answered by Yozzii last updated on 12/Apr/16
Let u=tan^(−1) y.⇒y=tanu (∗) Differentiating (∗) implicitly with respect to y gives 1=sec^2 u×(du/dy)⇒(du/dy)=(1/(sec^2 u)). According to the trigonometric identity, 1+tan^2 θ=sec^2 θ, we have that sec^2 u=tan^2 u+1. However, tanu=y. So, sec^2 u=1+y^2 and hence (du/dy)=(1/(y^2 +1)). Since (d/dy)(tan^(−1) y)=(1/(y^2 +1)) then d(tan^(−1) y)=(1/(y^2 +1))dy ⇒∫1d(tan^(−1) y)=∫(1/(y^2 +1))dy. Since ∫1dp=p+C where C is the constant of integration, ∫(1/(1+y^2 ))dy=tan^(−1) y+C.
$${Let}\:{u}={tan}^{−\mathrm{1}} {y}.\Rightarrow{y}={tanu}\:\:\left(\ast\right) \\ $$$${Differentiating}\:\left(\ast\right)\:{implicitly}\:{with} \\ $$$${respect}\:{to}\:{y}\:{gives}\: \\ $$$$\mathrm{1}={sec}^{\mathrm{2}} {u}×\frac{{du}}{{dy}}\Rightarrow\frac{{du}}{{dy}}=\frac{\mathrm{1}}{{sec}^{\mathrm{2}} {u}}. \\ $$$${According}\:{to}\:{the}\:{trigonometric}\:{identity}, \\ $$$$\mathrm{1}+{tan}^{\mathrm{2}} \theta={sec}^{\mathrm{2}} \theta,\:{we}\:{have}\:{that}\: \\ $$$${sec}^{\mathrm{2}} {u}={tan}^{\mathrm{2}} {u}+\mathrm{1}.\:{However},\:{tanu}={y}. \\ $$$${So},\:{sec}^{\mathrm{2}} {u}=\mathrm{1}+{y}^{\mathrm{2}} \:{and}\:{hence}\:\frac{{du}}{{dy}}=\frac{\mathrm{1}}{{y}^{\mathrm{2}} +\mathrm{1}}. \\ $$$${Since}\:\frac{{d}}{{dy}}\left({tan}^{−\mathrm{1}} {y}\right)=\frac{\mathrm{1}}{{y}^{\mathrm{2}} +\mathrm{1}}\:{then} \\ $$$$\:{d}\left({tan}^{−\mathrm{1}} {y}\right)=\frac{\mathrm{1}}{{y}^{\mathrm{2}} +\mathrm{1}}{dy} \\ $$$$\Rightarrow\int\mathrm{1}{d}\left({tan}^{−\mathrm{1}} {y}\right)=\int\frac{\mathrm{1}}{{y}^{\mathrm{2}} +\mathrm{1}}{dy}.\: \\ $$$${Since}\:\int\mathrm{1}{dp}={p}+{C}\:{where}\:{C}\:{is}\:{the}\: \\ $$$${constant}\:{of}\:{integration},\: \\ $$$$\int\frac{\mathrm{1}}{\mathrm{1}+{y}^{\mathrm{2}} }{dy}={tan}^{−\mathrm{1}} {y}+{C}. \\ $$$$ \\ $$
Answered by FilupSmith last updated on 13/Apr/16
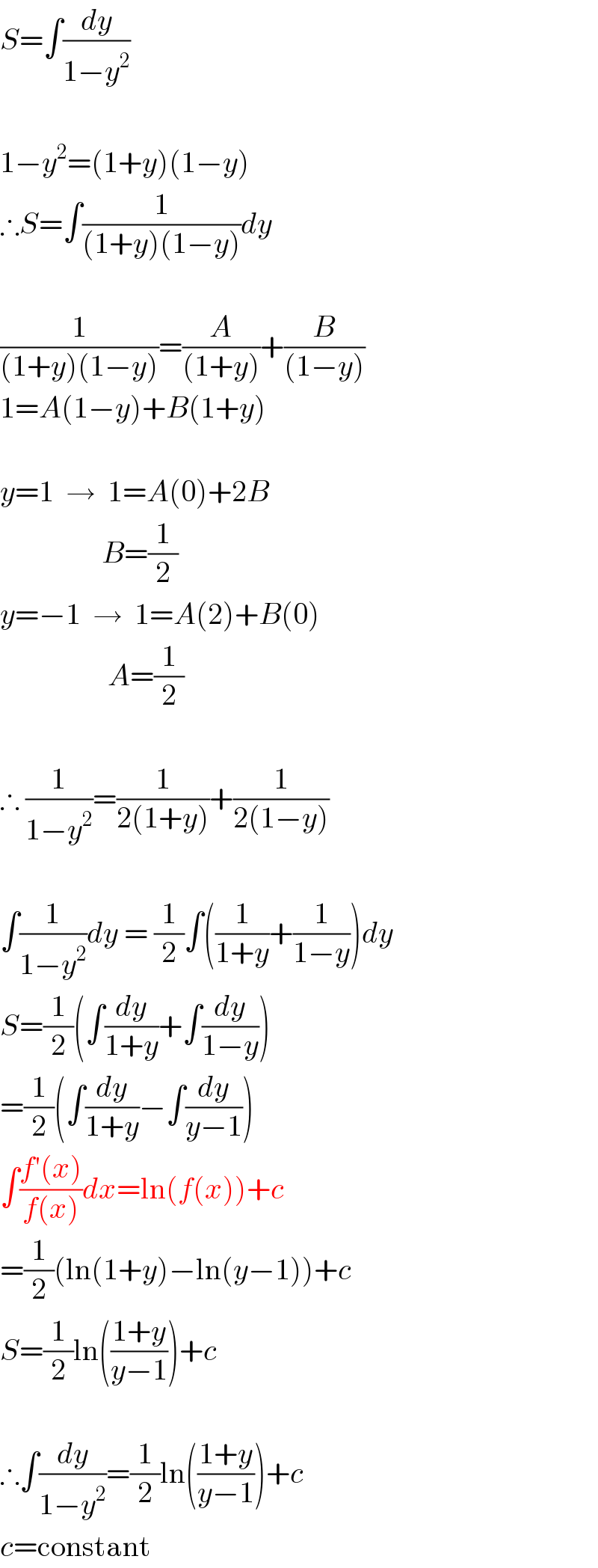
S=∫(dy/(1−y^2 )) 1−y^2 =(1+y)(1−y) ∴S=∫(1/((1+y)(1−y)))dy (1/((1+y)(1−y)))=(A/((1+y)))+(B/((1−y))) 1=A(1−y)+B(1+y) y=1 → 1=A(0)+2B B=(1/2) y=−1 → 1=A(2)+B(0) A=(1/2) ∴ (1/(1−y^2 ))=(1/(2(1+y)))+(1/(2(1−y))) ∫(1/(1−y^2 ))dy = (1/2)∫((1/(1+y))+(1/(1−y)))dy S=(1/2)(∫(dy/(1+y))+∫(dy/(1−y))) =(1/2)(∫(dy/(1+y))−∫(dy/(y−1))) ∫((f′(x))/(f(x)))dx=ln(f(x))+c =(1/2)(ln(1+y)−ln(y−1))+c S=(1/2)ln(((1+y)/(y−1)))+c ∴∫(dy/(1−y^2 ))=(1/2)ln(((1+y)/(y−1)))+c c=constant
$${S}=\int\frac{{dy}}{\mathrm{1}−{y}^{\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{1}−{y}^{\mathrm{2}} =\left(\mathrm{1}+{y}\right)\left(\mathrm{1}−{y}\right) \\ $$$$\therefore{S}=\int\frac{\mathrm{1}}{\left(\mathrm{1}+{y}\right)\left(\mathrm{1}−{y}\right)}{dy} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+{y}\right)\left(\mathrm{1}−{y}\right)}=\frac{{A}}{\left(\mathrm{1}+{y}\right)}+\frac{{B}}{\left(\mathrm{1}−{y}\right)} \\ $$$$\mathrm{1}={A}\left(\mathrm{1}−{y}\right)+{B}\left(\mathrm{1}+{y}\right) \\ $$$$ \\ $$$${y}=\mathrm{1}\:\:\rightarrow\:\:\mathrm{1}={A}\left(\mathrm{0}\right)+\mathrm{2}{B} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{B}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}=−\mathrm{1}\:\:\rightarrow\:\:\mathrm{1}={A}\left(\mathrm{2}\right)+{B}\left(\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{A}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\therefore\:\frac{\mathrm{1}}{\mathrm{1}−{y}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{y}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{y}\right)} \\ $$$$ \\ $$$$\int\frac{\mathrm{1}}{\mathrm{1}−{y}^{\mathrm{2}} }{dy}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\mathrm{1}+{y}}+\frac{\mathrm{1}}{\mathrm{1}−{y}}\right){dy} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\left(\int\frac{{dy}}{\mathrm{1}+{y}}+\int\frac{{dy}}{\mathrm{1}−{y}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\int\frac{{dy}}{\mathrm{1}+{y}}−\int\frac{{dy}}{{y}−\mathrm{1}}\right) \\ $$$$\int\frac{{f}'\left({x}\right)}{{f}\left({x}\right)}{dx}=\mathrm{ln}\left({f}\left({x}\right)\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\left(\mathrm{1}+{y}\right)−\mathrm{ln}\left({y}−\mathrm{1}\right)\right)+{c} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}+{y}}{{y}−\mathrm{1}}\right)+{c} \\ $$$$ \\ $$$$\therefore\int\frac{{dy}}{\mathrm{1}−{y}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}+{y}}{{y}−\mathrm{1}}\right)+{c} \\ $$$${c}=\mathrm{constant} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *