Question Number 1030 by 123456 last updated on 20/May/15
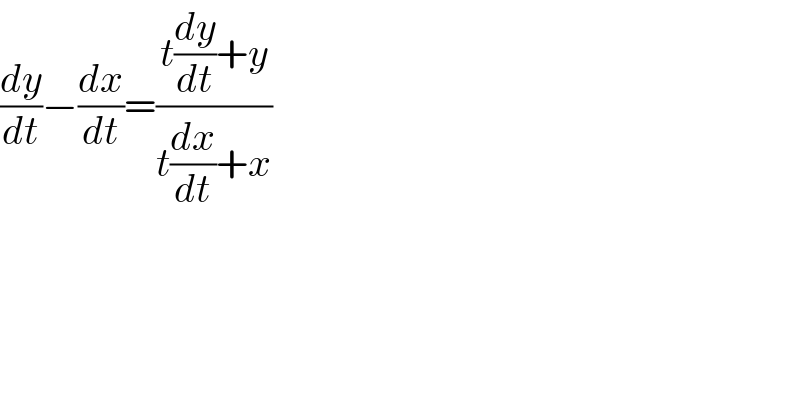
$$\frac{{dy}}{{dt}}−\frac{{dx}}{{dt}}=\frac{{t}\frac{{dy}}{{dt}}+{y}}{{t}\frac{{dx}}{{dt}}+{x}} \\ $$
Answered by prakash jain last updated on 21/May/15
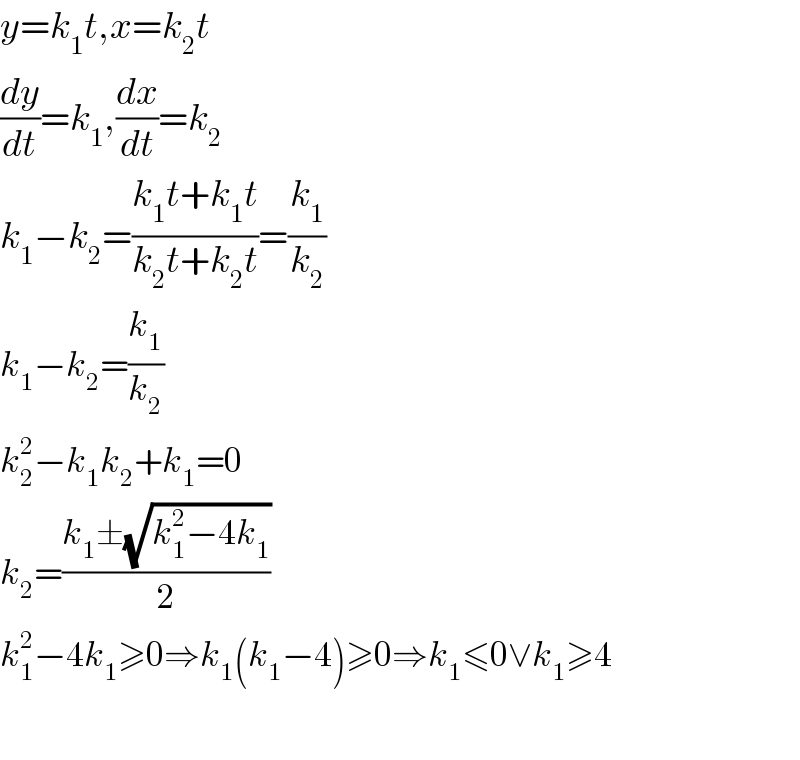
$${y}={k}_{\mathrm{1}} {t},{x}={k}_{\mathrm{2}} {t} \\ $$$$\frac{{dy}}{{dt}}={k}_{\mathrm{1}} ,\frac{{dx}}{{dt}}={k}_{\mathrm{2}} \\ $$$${k}_{\mathrm{1}} −{k}_{\mathrm{2}} =\frac{{k}_{\mathrm{1}} {t}+{k}_{\mathrm{1}} {t}}{{k}_{\mathrm{2}} {t}+{k}_{\mathrm{2}} {t}}=\frac{{k}_{\mathrm{1}} }{{k}_{\mathrm{2}} } \\ $$$${k}_{\mathrm{1}} −{k}_{\mathrm{2}} =\frac{{k}_{\mathrm{1}} }{{k}_{\mathrm{2}} } \\ $$$${k}_{\mathrm{2}} ^{\mathrm{2}} −{k}_{\mathrm{1}} {k}_{\mathrm{2}} +{k}_{\mathrm{1}} =\mathrm{0} \\ $$$${k}_{\mathrm{2}} =\frac{{k}_{\mathrm{1}} \pm\sqrt{{k}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{4}{k}_{\mathrm{1}} }}{\mathrm{2}} \\ $$$${k}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{4}{k}_{\mathrm{1}} \geqslant\mathrm{0}\Rightarrow{k}_{\mathrm{1}} \left({k}_{\mathrm{1}} −\mathrm{4}\right)\geqslant\mathrm{0}\Rightarrow{k}_{\mathrm{1}} \leqslant\mathrm{0}\vee{k}_{\mathrm{1}} \geqslant\mathrm{4} \\ $$$$ \\ $$
