Question Number 9461 by tawakalitu last updated on 09/Dec/16
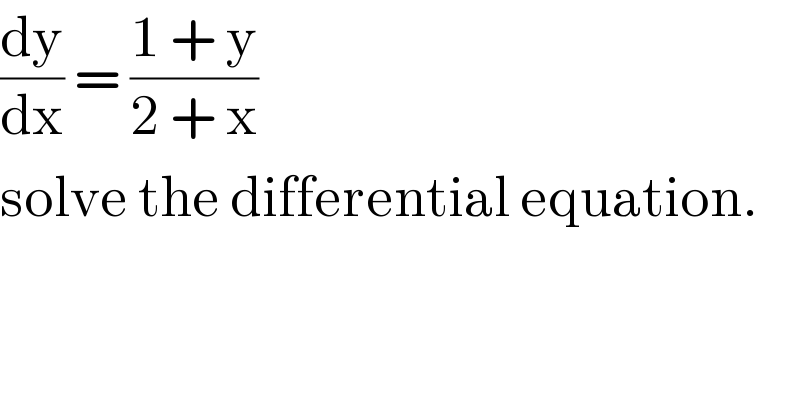
$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{1}\:+\:\mathrm{y}}{\mathrm{2}\:+\:\mathrm{x}} \\ $$$$\mathrm{solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation}. \\ $$
Answered by mrW last updated on 09/Dec/16
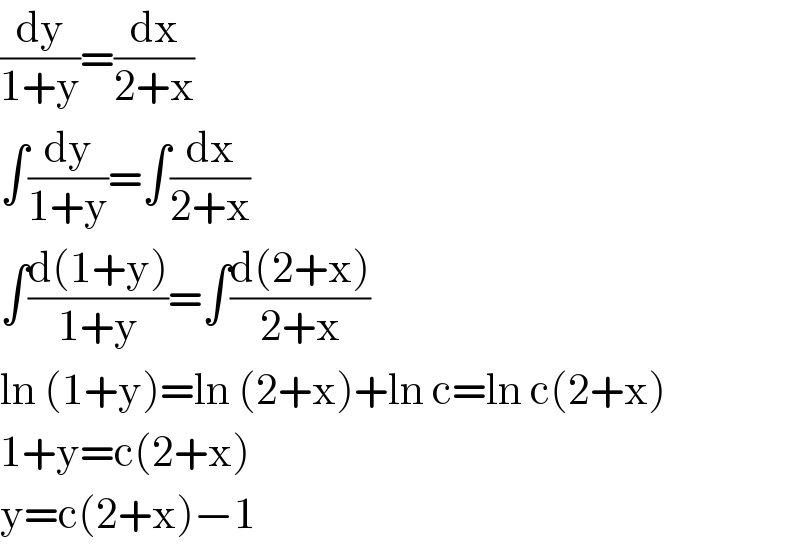
$$\frac{\mathrm{dy}}{\mathrm{1}+\mathrm{y}}=\frac{\mathrm{dx}}{\mathrm{2}+\mathrm{x}} \\ $$$$\int\frac{\mathrm{dy}}{\mathrm{1}+\mathrm{y}}=\int\frac{\mathrm{dx}}{\mathrm{2}+\mathrm{x}} \\ $$$$\int\frac{\mathrm{d}\left(\mathrm{1}+\mathrm{y}\right)}{\mathrm{1}+\mathrm{y}}=\int\frac{\mathrm{d}\left(\mathrm{2}+\mathrm{x}\right)}{\mathrm{2}+\mathrm{x}} \\ $$$$\mathrm{ln}\:\left(\mathrm{1}+\mathrm{y}\right)=\mathrm{ln}\:\left(\mathrm{2}+\mathrm{x}\right)+\mathrm{ln}\:\mathrm{c}=\mathrm{ln}\:\mathrm{c}\left(\mathrm{2}+\mathrm{x}\right) \\ $$$$\mathrm{1}+\mathrm{y}=\mathrm{c}\left(\mathrm{2}+\mathrm{x}\right) \\ $$$$\mathrm{y}=\mathrm{c}\left(\mathrm{2}+\mathrm{x}\right)−\mathrm{1} \\ $$
Commented by tawakalitu last updated on 09/Dec/16
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
