Question Number 142344 by mnjuly1970 last updated on 30/May/21
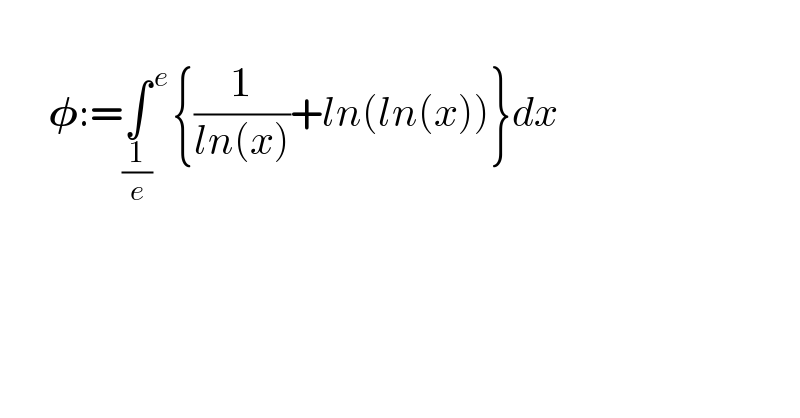
$$ \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}:=\underset{\frac{\mathrm{1}}{{e}}} {\int}^{\:{e}} \left\{\frac{\mathrm{1}}{{ln}\left({x}\right)}+{ln}\left({ln}\left({x}\right)\right)\right\}{dx} \\ $$
Commented by Dwaipayan Shikari last updated on 30/May/21
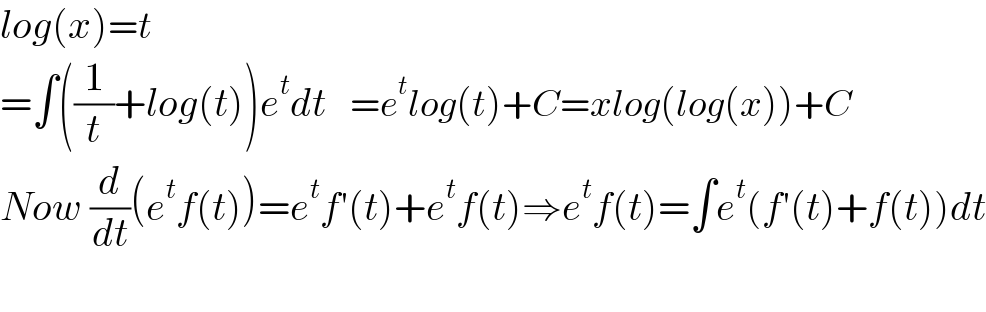
$${log}\left({x}\right)={t} \\ $$$$=\int\left(\frac{\mathrm{1}}{{t}}+{log}\left({t}\right)\right){e}^{{t}} {dt}\:\:\:={e}^{{t}} {log}\left({t}\right)+{C}={xlog}\left({log}\left({x}\right)\right)+{C} \\ $$$${Now}\:\frac{{d}}{{dt}}\left({e}^{{t}} {f}\left({t}\right)\right)={e}^{{t}} {f}'\left({t}\right)+{e}^{{t}} {f}\left({t}\right)\Rightarrow{e}^{{t}} {f}\left({t}\right)=\int{e}^{{t}} \left({f}'\left({t}\right)+{f}\left({t}\right)\right){dt} \\ $$$$ \\ $$
Commented by rs4089 last updated on 30/May/21
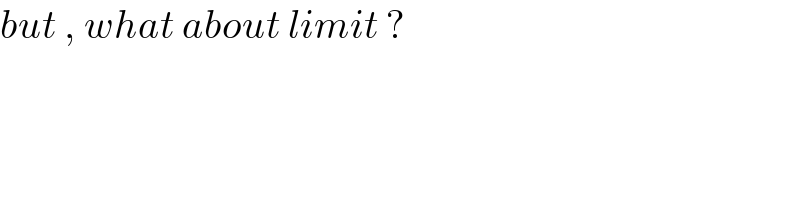
$${but}\:,\:{what}\:{about}\:{limit}\:? \\ $$
Commented by Dwaipayan Shikari last updated on 30/May/21

$${log}\left({log}\left({x}\right)\right)\:{is}\:{not}\:{defined}\:{at}\:\frac{\mathrm{1}}{{e}} \\ $$$${log}\left({log}\left(\frac{\mathrm{1}}{{e}}\right)\right)={log}\left(−\mathrm{1}\right)={i}\pi\: \\ $$
