Question Number 66185 by Tony Lin last updated on 10/Aug/19

$$\left({e}^{\frac{\mathrm{1}}{{e}}} \right)^{\left({e}^{\frac{\mathrm{1}}{{e}}} \right)^{.\centerdot^{.\left({e}^{\frac{\mathrm{1}}{{e}}} \right)} } } =? \\ $$
Commented by GordonYeeman last updated on 10/Aug/19

$$\left({e}^{\frac{\mathrm{1}}{{e}}} \right)^{{x}} ={x} \\ $$$$\frac{{x}}{{e}}{lne}={lnx} \\ $$$$\frac{{lne}}{{e}}=\frac{{lnx}}{{x}}\rightarrow{x}={e} \\ $$
Answered by mr W last updated on 10/Aug/19
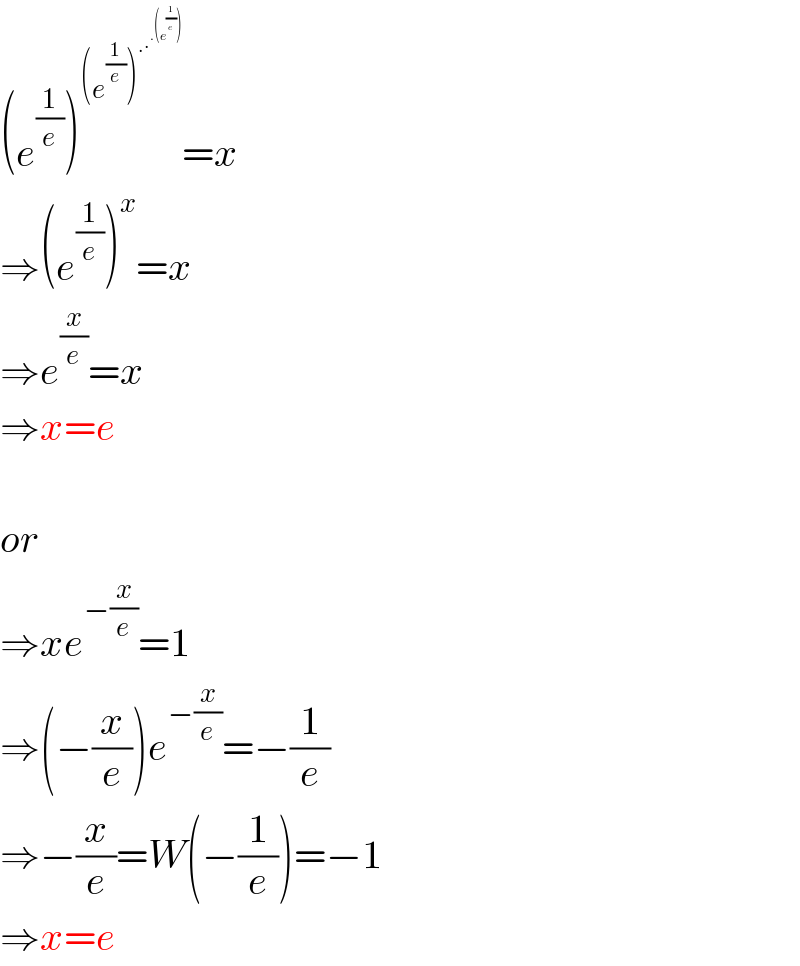
$$\left({e}^{\frac{\mathrm{1}}{{e}}} \right)^{\left({e}^{\frac{\mathrm{1}}{{e}}} \right)^{.\centerdot^{.\left({e}^{\frac{\mathrm{1}}{{e}}} \right)} } } ={x} \\ $$$$\Rightarrow\left({e}^{\frac{\mathrm{1}}{{e}}} \right)^{{x}} ={x} \\ $$$$\Rightarrow{e}^{\frac{{x}}{{e}}} ={x} \\ $$$$\Rightarrow{x}={e} \\ $$$$ \\ $$$${or} \\ $$$$\Rightarrow{xe}^{−\frac{{x}}{{e}}} =\mathrm{1} \\ $$$$\Rightarrow\left(−\frac{{x}}{{e}}\right){e}^{−\frac{{x}}{{e}}} =−\frac{\mathrm{1}}{{e}} \\ $$$$\Rightarrow−\frac{{x}}{{e}}={W}\left(−\frac{\mathrm{1}}{{e}}\right)=−\mathrm{1} \\ $$$$\Rightarrow{x}={e} \\ $$
