Question Number 140506 by Dwaipayan Shikari last updated on 08/May/21

$${e}^{\left(\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{3}}+\frac{\zeta\left(\mathrm{4}\right)}{\mathrm{4}}−\frac{\zeta\left(\mathrm{5}\right)}{\mathrm{5}}+…\right)} \:\:\:=? \\ $$
Answered by mnjuly1970 last updated on 08/May/21

Commented by mnjuly1970 last updated on 08/May/21
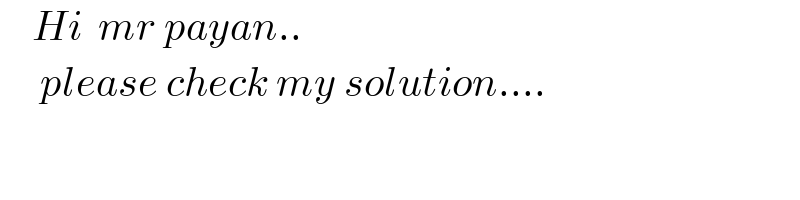
$$\:\:\:\:{Hi}\:\:{mr}\:{payan}.. \\ $$$$\:\:\:\:\:{please}\:{check}\:{my}\:{solution}…. \\ $$$$\:\:\:\:\: \\ $$
Commented by Dwaipayan Shikari last updated on 08/May/21
$${Correct}\:{sir}\:!\:{Great}! \\ $$
Commented by Niiicooooo last updated on 08/May/21

$${nice}\:{proof}! \\ $$
Commented by mnjuly1970 last updated on 08/May/21

$$\:\:{mercey}… \\ $$
Answered by Dwaipayan Shikari last updated on 08/May/21
![ψ(z+1)=ψ(1)+((ψ′(1))/(1!))z+((ψ′′(1))/(2!))z^2 +... ⇒ψ(z+1)=−γ+ζ(2)z−ζ(3)z^2 +ζ(4)z^3 −... ⇒∫_0 ^1 ψ(z+1)dz=−γ+∫_0 ^1 ζ(2)z−ζ(3)z^2 +..dz ⇒[log(Γ(z+1))]_0 ^1 +γ=((ζ(2))/2)−((ζ(3))/3)+((ζ(4))/4)−.. γ=((ζ(2))/2)−((ζ(3))/3)+...](https://www.tinkutara.com/question/Q140516.png)
$$\psi\left({z}+\mathrm{1}\right)=\psi\left(\mathrm{1}\right)+\frac{\psi'\left(\mathrm{1}\right)}{\mathrm{1}!}{z}+\frac{\psi''\left(\mathrm{1}\right)}{\mathrm{2}!}{z}^{\mathrm{2}} +… \\ $$$$\Rightarrow\psi\left({z}+\mathrm{1}\right)=−\gamma+\zeta\left(\mathrm{2}\right){z}−\zeta\left(\mathrm{3}\right){z}^{\mathrm{2}} +\zeta\left(\mathrm{4}\right){z}^{\mathrm{3}} −… \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \psi\left({z}+\mathrm{1}\right){dz}=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \zeta\left(\mathrm{2}\right){z}−\zeta\left(\mathrm{3}\right){z}^{\mathrm{2}} +..{dz} \\ $$$$\Rightarrow\left[{log}\left(\Gamma\left({z}+\mathrm{1}\right)\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\gamma=\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{3}}+\frac{\zeta\left(\mathrm{4}\right)}{\mathrm{4}}−.. \\ $$$$\gamma=\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{3}}+… \\ $$
Commented by mnjuly1970 last updated on 08/May/21

$${nice}\:{very}\:{nice}… \\ $$
