Question Number 8486 by PradipGos. last updated on 12/Oct/16
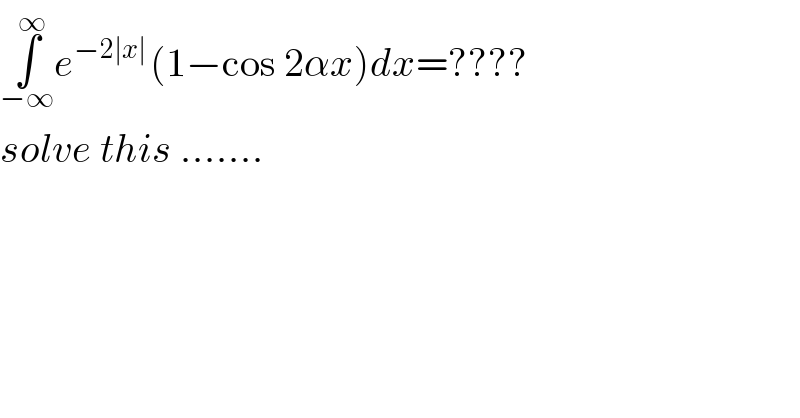
$$\underset{−\infty} {\overset{\infty} {\int}}{e}^{−\mathrm{2}\mid{x}\overset{} {\mid}\:} \left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\alpha{x}\right){dx}=???? \\ $$$${solve}\:{this}\:……. \\ $$$$ \\ $$$$ \\ $$
Answered by Yozzias last updated on 12/Oct/16
![I=∫_(−∞) ^∞ e^(−2∣x∣) (1−cos2αx)dx Since ∣x∣= { ((x x≥0)),((−x x<0)) :} ∣x∣=x for x∈[0,∞) and ∣x∣=−x for x∈(−∞,0]. ∴I=∫_0 ^∞ e^(−2x) (1−cos2αx)dx+∫^0 _(−∞) e^(2x) (1−cos2αx)dx Let J=∫e^(ax) (1−cos2αx)dx (a≠0) J=(1/a)e^(ax) (1−cos2αx)−∫(1/a)e^(ax) (2αsin2αx)dx J=((e^(ax) (1−cos2αx))/a)−((2α)/a)∫e^(ax) sin2αxdx J=((e^(ax) (1−cos2αx))/a)−((2α)/a)[(1/a)e^(ax) sin2αx−∫(1/a)e^(ax) 2αcos2αxdx] J=((e^(ax) (1−cos2αx))/a)−((2αe^(ax) sin2αx)/a^2 )+((4α^2 )/a^2 )∫e^(ax) cos2αxdx. Now, ∫e^(ax) cos2αxdx=∫e^(ax) dx−J=(1/a)e^(ax) −J. ∴J=((e^(ax) (1−cos2αx))/a)−((2αe^(ax) sin2αx)/a^2 )+((4α^2 )/a^3 )e^(ax) −((4α^2 )/a^2 )J J=((a^2 e^(ax) )/(a^2 +4α^2 )){((1−cos2αx)/a)−((2αsin2αx)/a^2 )+((4α^2 )/a^3 )}+C Let a=−2. ∴ J∣_0 ^∞ =((4e^(−2x) )/(4+4α^2 )){((1−cos2αx)/(−2))−((2αsin2αx)/4)−(α^2 /2)}∣_0 ^∞ J∣_0 ^∞ =0−((4×1)/(4+4α^2 )){((1−1)/(−2))−(0/4)−(α^2 /2)}=(α^2 /(2(1+α^2 ))) Let a=2. ∴ J∣_(−∞) ^0 =(e^(2x) /(1+α^2 )){((1−cos2αx)/2)−((2αsin2αx)/4)+((4α^2 )/8)}∣_(−∞) ^0 =(α^2 /(2(1+α^2 ))) ∴ I=2×(α^2 /(2(1+α^2 )))=(α^2 /(α^2 +1))](https://www.tinkutara.com/question/Q8487.png)
$$\mathrm{I}=\int_{−\infty} ^{\infty} \mathrm{e}^{−\mathrm{2}\mid\mathrm{x}\mid} \left(\mathrm{1}−\mathrm{cos2}\alpha\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{Since}\:\mid\mathrm{x}\mid=\begin{cases}{\mathrm{x}\:\:\:\:\:\:\:\:\:\:\mathrm{x}\geqslant\mathrm{0}}\\{−\mathrm{x}\:\:\:\:\:\:\mathrm{x}<\mathrm{0}}\end{cases} \\ $$$$\mid\mathrm{x}\mid=\mathrm{x}\:\mathrm{for}\:\mathrm{x}\in\left[\mathrm{0},\infty\right)\:\mathrm{and}\:\mid\mathrm{x}\mid=−\mathrm{x}\:\mathrm{for}\:\mathrm{x}\in\left(−\infty,\mathrm{0}\right]. \\ $$$$\therefore\mathrm{I}=\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{1}−\mathrm{cos2}\alpha\mathrm{x}\right)\mathrm{dx}+\underset{−\infty} {\int}^{\mathrm{0}} \mathrm{e}^{\mathrm{2x}} \left(\mathrm{1}−\mathrm{cos2}\alpha\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{Let}\:\mathrm{J}=\int\mathrm{e}^{\mathrm{ax}} \left(\mathrm{1}−\mathrm{cos2}\alpha\mathrm{x}\right)\mathrm{dx}\:\:\left(\mathrm{a}\neq\mathrm{0}\right) \\ $$$$\mathrm{J}=\frac{\mathrm{1}}{\mathrm{a}}\mathrm{e}^{\mathrm{ax}} \left(\mathrm{1}−\mathrm{cos2}\alpha\mathrm{x}\right)−\int\frac{\mathrm{1}}{\mathrm{a}}\mathrm{e}^{\mathrm{ax}} \left(\mathrm{2}\alpha\mathrm{sin2}\alpha\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{J}=\frac{\mathrm{e}^{\mathrm{ax}} \left(\mathrm{1}−\mathrm{cos2}\alpha\mathrm{x}\right)}{\mathrm{a}}−\frac{\mathrm{2}\alpha}{\mathrm{a}}\int\mathrm{e}^{\mathrm{ax}} \mathrm{sin2}\alpha\mathrm{xdx} \\ $$$$\mathrm{J}=\frac{\mathrm{e}^{\mathrm{ax}} \left(\mathrm{1}−\mathrm{cos2}\alpha\mathrm{x}\right)}{\mathrm{a}}−\frac{\mathrm{2}\alpha}{\mathrm{a}}\left[\frac{\mathrm{1}}{\mathrm{a}}\mathrm{e}^{\mathrm{ax}} \mathrm{sin2}\alpha\mathrm{x}−\int\frac{\mathrm{1}}{\mathrm{a}}\mathrm{e}^{\mathrm{ax}} \mathrm{2}\alpha\mathrm{cos2}\alpha\mathrm{xdx}\right] \\ $$$$\mathrm{J}=\frac{\mathrm{e}^{\mathrm{ax}} \left(\mathrm{1}−\mathrm{cos2}\alpha\mathrm{x}\right)}{\mathrm{a}}−\frac{\mathrm{2}\alpha\mathrm{e}^{\mathrm{ax}} \mathrm{sin2}\alpha\mathrm{x}}{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{4}\alpha^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }\int\mathrm{e}^{\mathrm{ax}} \mathrm{cos2}\alpha\mathrm{xdx}. \\ $$$$\mathrm{Now},\:\int\mathrm{e}^{\mathrm{ax}} \mathrm{cos2}\alpha\mathrm{xdx}=\int\mathrm{e}^{\mathrm{ax}} \mathrm{dx}−\mathrm{J}=\frac{\mathrm{1}}{\mathrm{a}}\mathrm{e}^{\mathrm{ax}} −\mathrm{J}. \\ $$$$\therefore\mathrm{J}=\frac{\mathrm{e}^{\mathrm{ax}} \left(\mathrm{1}−\mathrm{cos2}\alpha\mathrm{x}\right)}{\mathrm{a}}−\frac{\mathrm{2}\alpha\mathrm{e}^{\mathrm{ax}} \mathrm{sin2}\alpha\mathrm{x}}{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{4}\alpha^{\mathrm{2}} }{\mathrm{a}^{\mathrm{3}} }\mathrm{e}^{\mathrm{ax}} −\frac{\mathrm{4}\alpha^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }\mathrm{J} \\ $$$$\mathrm{J}=\frac{\mathrm{a}^{\mathrm{2}} \mathrm{e}^{\mathrm{ax}} }{\mathrm{a}^{\mathrm{2}} +\mathrm{4}\alpha^{\mathrm{2}} }\left\{\frac{\mathrm{1}−\mathrm{cos2}\alpha\mathrm{x}}{\mathrm{a}}−\frac{\mathrm{2}\alpha\mathrm{sin2}\alpha\mathrm{x}}{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{4}\alpha^{\mathrm{2}} }{\mathrm{a}^{\mathrm{3}} }\right\}+\mathrm{C} \\ $$$$\mathrm{Let}\:\mathrm{a}=−\mathrm{2}.\:\therefore\:\:\mathrm{J}\mid_{\mathrm{0}} ^{\infty} =\frac{\mathrm{4e}^{−\mathrm{2x}} }{\mathrm{4}+\mathrm{4}\alpha^{\mathrm{2}} }\left\{\frac{\mathrm{1}−\mathrm{cos2}\alpha\mathrm{x}}{−\mathrm{2}}−\frac{\mathrm{2}\alpha\mathrm{sin2}\alpha\mathrm{x}}{\mathrm{4}}−\frac{\alpha^{\mathrm{2}} }{\mathrm{2}}\right\}\mid_{\mathrm{0}} ^{\infty} \\ $$$$\mathrm{J}\mid_{\mathrm{0}} ^{\infty} =\mathrm{0}−\frac{\mathrm{4}×\mathrm{1}}{\mathrm{4}+\mathrm{4}\alpha^{\mathrm{2}} }\left\{\frac{\mathrm{1}−\mathrm{1}}{−\mathrm{2}}−\frac{\mathrm{0}}{\mathrm{4}}−\frac{\alpha^{\mathrm{2}} }{\mathrm{2}}\right\}=\frac{\alpha^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)} \\ $$$$\mathrm{Let}\:\mathrm{a}=\mathrm{2}.\:\therefore\:\mathrm{J}\mid_{−\infty} ^{\mathrm{0}} =\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{1}+\alpha^{\mathrm{2}} }\left\{\frac{\mathrm{1}−\mathrm{cos2}\alpha\mathrm{x}}{\mathrm{2}}−\frac{\mathrm{2}\alpha\mathrm{sin2}\alpha\mathrm{x}}{\mathrm{4}}+\frac{\mathrm{4}\alpha^{\mathrm{2}} }{\mathrm{8}}\right\}\mid_{−\infty} ^{\mathrm{0}} =\frac{\alpha^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)} \\ $$$$\therefore\:\mathrm{I}=\mathrm{2}×\frac{\alpha^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}=\frac{\alpha^{\mathrm{2}} }{\alpha^{\mathrm{2}} +\mathrm{1}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by PradipGos. last updated on 13/Oct/16

$$\mathrm{Thanks} \\ $$
