Question Number 12744 by tawa last updated on 30/Apr/17
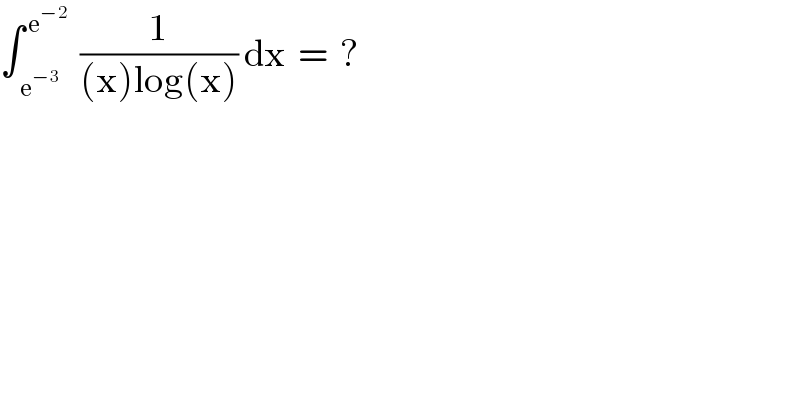
$$\int_{\:\mathrm{e}^{−\mathrm{3}} } ^{\:\mathrm{e}^{−\mathrm{2}} } \:\:\frac{\mathrm{1}}{\left(\mathrm{x}\right)\mathrm{log}\left(\mathrm{x}\right)}\:\mathrm{dx}\:\:=\:\:? \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/Apr/17
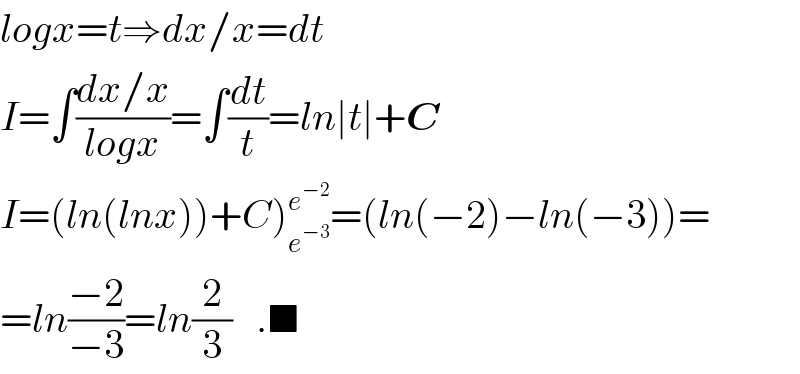
$${logx}={t}\Rightarrow{dx}/{x}={dt} \\ $$$${I}=\int\frac{{dx}/{x}}{{logx}}=\int\frac{{dt}}{{t}}={ln}\mid{t}\mid+\boldsymbol{{C}} \\ $$$$\left.{I}=\left({ln}\left({lnx}\right)\right)+{C}\right)_{{e}^{−\mathrm{3}} } ^{{e}^{−\mathrm{2}} } =\left({ln}\left(−\mathrm{2}\right)−{ln}\left(−\mathrm{3}\right)\right)= \\ $$$$={ln}\frac{−\mathrm{2}}{−\mathrm{3}}={ln}\frac{\mathrm{2}}{\mathrm{3}}\:\:\:.\blacksquare \\ $$
Commented by tawa last updated on 30/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
